"使用lasso进行线性回归的收缩和选择方法"

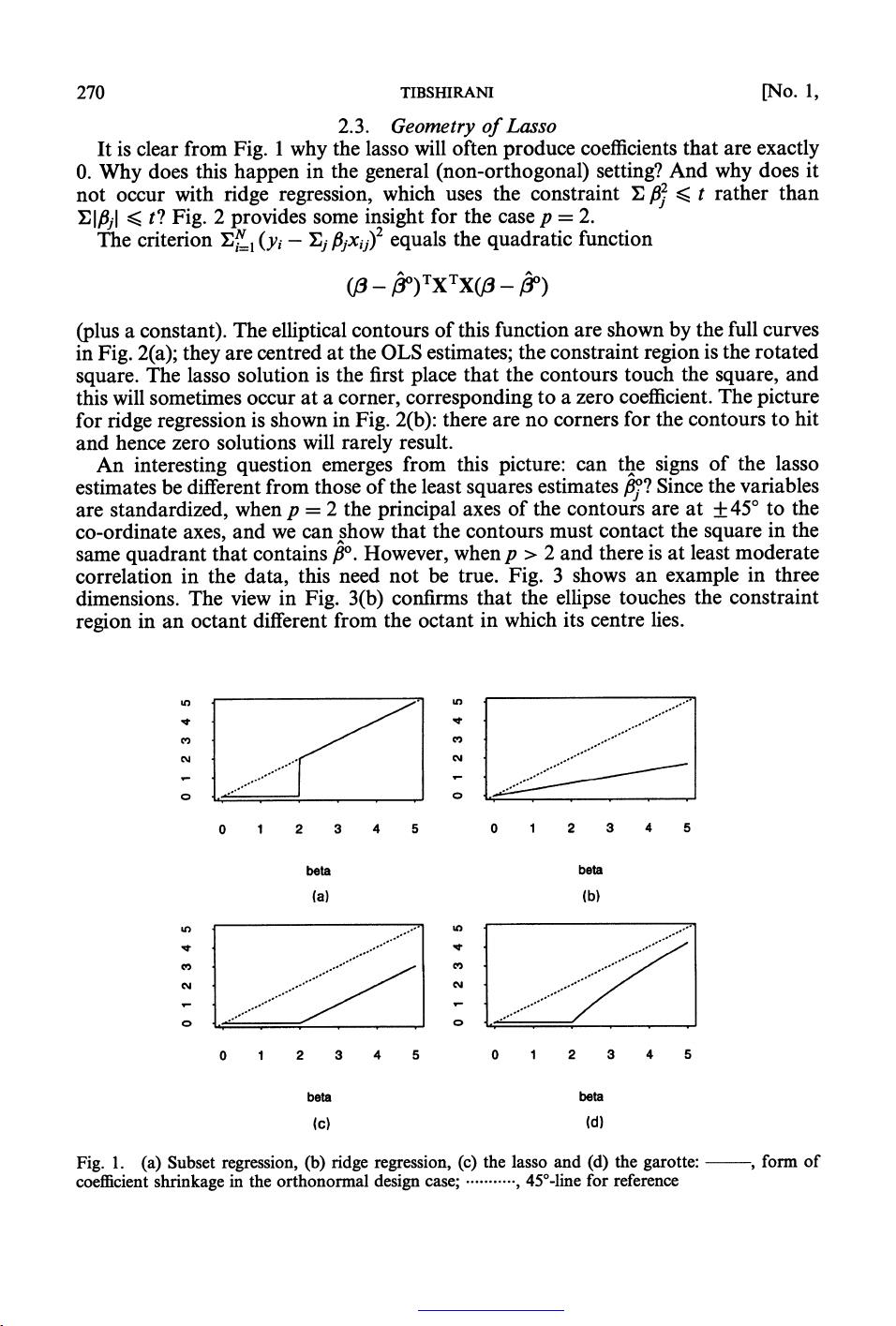
Regression Shrinkage and Selection via the Lasso is a groundbreaking paper written by Robert Tibshirani in 1996, published in the Journal of the Royal Statistical Society. The paper introduces the method of using lasso regression for shrinking and selecting variables in linear regression models. The lasso stands for Least Absolute Shrinkage and Selection Operator, and it is a regularization technique that can help improve the accuracy and interpretability of linear regression models. The key idea behind lasso regression is to add a penalty term to the traditional least squares loss function, where the penalty is the sum of the absolute values of the coefficients multiplied by a tuning parameter lambda. This penalty term encourages sparsity in the coefficients, effectively shrinking some coefficients towards zero and setting others to exactly zero. As a result, lasso regression can perform feature selection by identifying and discarding irrelevant variables from the model. Tibshirani demonstrates the effectiveness of lasso regression through simulations and real data examples, showing how it can outperform traditional methods in terms of predictive accuracy and model interpretability. The paper also discusses the computational challenges of implementing lasso regression and proposes efficient algorithms for solving the optimization problem. Overall, Regression Shrinkage and Selection via the Lasso has had a significant impact on the field of statistics and data analysis. It has popularized the use of lasso regression as a powerful tool for variable selection and model regularization, leading to numerous applications in machine learning, econometrics, and other domains. The paper continues to be widely cited and referenced in research literature, cementing its status as a seminal work in the field of statistical methodology.