数据结构排序算法详解：quicksort、heapsort与hoaresort实践

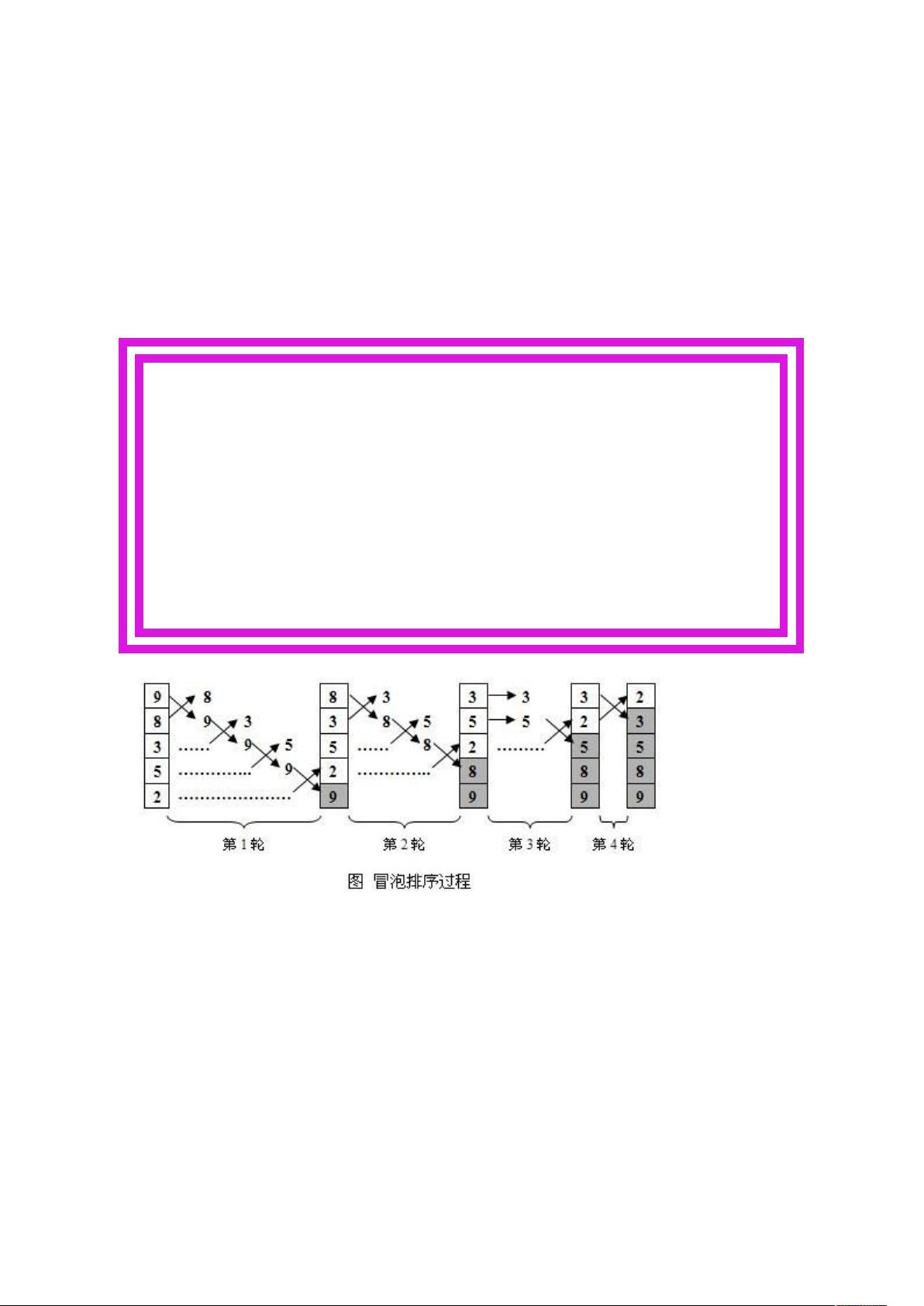
本文主要介绍了数据结构中几种常见的排序算法的概述、时间复杂度、空间复杂度以及它们的特点。以下是详细的解析： 1. 冒泡排序: - 时间复杂度：平均情况、最好情况、最坏情况均为 O(n^2)，其中最好情况发生在已经排序好的数组上，而最坏情况是逆序数组。 - 空间复杂度：O(1)，因为原地排序，不需要额外存储空间。 - 稳定性：冒泡排序是稳定的，相同元素的相对顺序不会改变。 - 代码实现和工作原理：通过两层嵌套循环，每次比较相邻元素并交换，较小的元素逐渐“浮”到数组前端。 2. 直接插入排序： - 时间复杂度：同样为 O(n^2)，但在近乎有序的数组中效率较高。 - 空间复杂度：O(1)。 - 稳定性：也是稳定的，因为当遇到相等元素时，会保持原有的相对位置。 - 代码实现：逐个元素插入到已排序部分的正确位置。 3. 希尔排序（Shell sort）： - 时间复杂度：平均和最坏情况下为 O(n^(1.25))，在特定步长序列下性能可能接近 O(nlogn)。 - 空间复杂度：O(1)。 - 稳定性：不稳定。 - 代码实现：是一种改进的插入排序，通过设置不同的间隔序列进行插入排序。 4. 随机快速排序 (Randomized Quick Sort)： - 时间复杂度：平均和最好的情况下为 O(nlogn)，最坏情况下为 O(n^2)，但这种情况非常罕见。 - 空间复杂度：平均 O(logn)，最坏情况下 O(n)。 - 稳定性：不稳定。 - 工作原理：随机选择一个元素作为基准，分割数组并递归地对左右子数组进行快速排序。 5. 快速排序 (Heap Sort)： - 时间复杂度：平均和最坏情况均为 O(nlogn)，空间复杂度为 O(nlogn)。 - 稳定性：不稳定。 - 代码实现：利用堆数据结构进行排序，首先将数组构建成大顶堆，然后不断取出最大元素放到正确位置。 6. 归并排序 (Merge Sort)： - 时间复杂度：无论哪种情况都是 O(nlogn)。 - 空间复杂度：O(nlogn)。 - 稳定性：稳定。 - 工作原理：采用分治策略，先将数组一分为二，然后递归地排序子数组，最后合并两个有序数组。 7. 堆排序 (Heap Sort)： - 时间复杂度：同样为 O(nlogn)。 - 空间复杂度：O(nlogn)。 - 稳定性：不稳定。 - 代码实现：构建最大堆后，每次取出堆顶元素放到正确位置，调整堆使其恢复大顶堆。 这些排序算法各有优缺点，适用于不同的场景。理解这些基础排序算法有助于在实际编程中根据具体需求选择合适的排序方法。同时，作者通过编写代码和绘制图表的方式，使得抽象的概念更易于理解和记忆。