奇异值分解（SVD）在矩阵变换中的应用

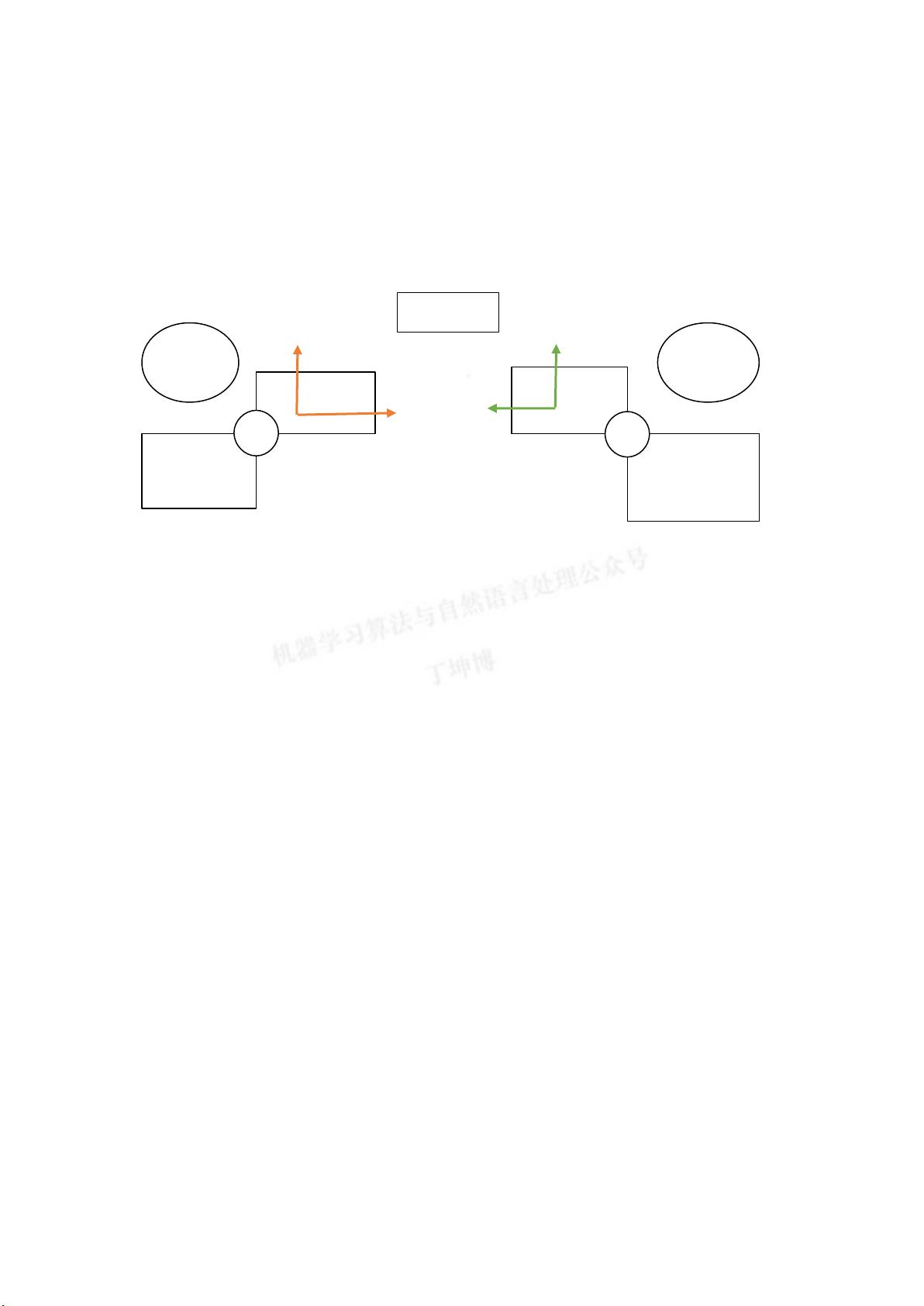
线性代数301 线性代数是数学中一个重要的分支，它广泛应用于各个领域，包括机器学习、数据挖掘、计算机视觉、自然语言处理等。线性代数的核心内容包括向量空间、矩阵、线性变换、奇异值分解等。 奇异值分解（Singular Value Decomposition，SVD）是线性代数中一个重要的概念，它可以将矩阵分解成三个矩阵的乘积，分别是两个正交矩阵和一个对角矩阵。SVD有很多实际应用，例如数据降维、图像压缩、文本分析等。 在本节中，我们将详细介绍奇异值分解的定义、矩阵形式和计算方法。 **2.1 基变换** 奇异值分解的基本思想是将矩阵A分解成三个矩阵的乘积，即U、Σ和V。其中，U和V是两个正交矩阵，Σ是一个对角矩阵。这个过程可以看作是将行空间的一组正交基变换成列空间里的一组正交基。 **2.2 矩阵形式** 我们可以用矩阵形式来表示奇异值分解的过程。假设矩阵A是一个m*n矩阵，那么我们可以将其分解成： A = U Σ V^T 其中，U是一个m*r矩阵，Σ是一个r*r矩阵，V是一个n*r矩阵。r是矩阵A的秩。 **2.3 计算方法** 计算奇异值分解的方法有很多，例如可以使用 Gram-Schmidt Process 来计算正交基。然而，在实际应用中，我们通常使用变形技巧来简化求解过程。 例如，我们可以使用A^T A运算来消去U，得到： A^T A = V Σ^2 V^T 然后，我们可以使用Eigenvalue Decomposition来计算V和Σ。 类似地，我们可以使用A A^T运算来消去V，得到： A A^T = U Σ^2 U^T 然后，我们可以使用Eigenvalue Decomposition来计算U和Σ。 奇异值分解是线性代数中一个重要的概念，它有很多实际应用。通过学习奇异值分解，我们可以更好地理解矩阵的结构和性质，并且可以应用于机器学习、数据挖掘、计算机视觉等领域。