最小二乘法：误差平方和的拟合优化

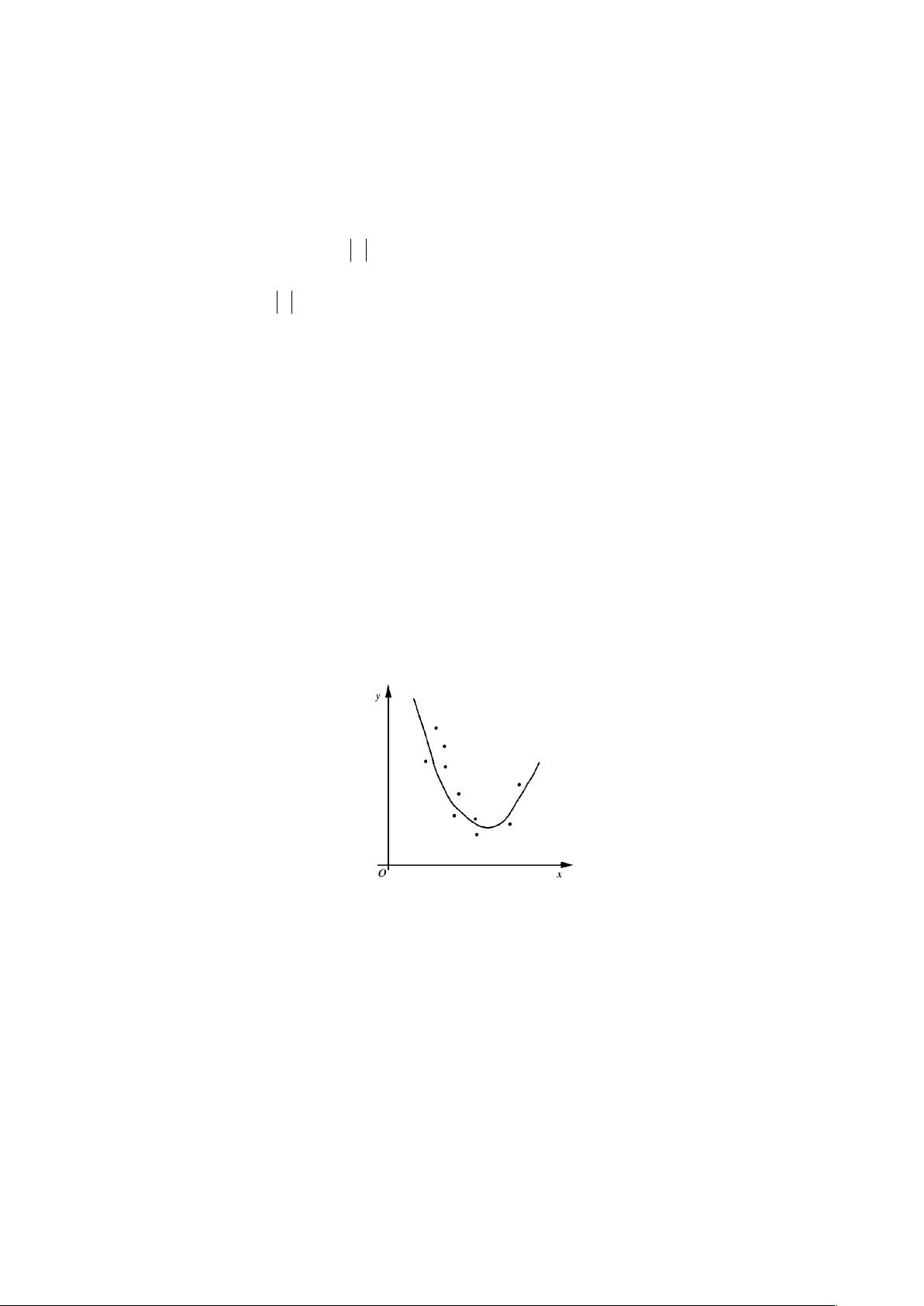
最小二乘法是一种常用的数学优化技术，在统计学、机器学习和数据分析等领域中广泛应用，特别是在曲线拟合和数据拟合过程中。其基本原理是通过寻找一个函数，使其与一组给定数据点之间的误差平方和达到最小，以此来近似数据的内在规律。 首先，最小二乘法关注的是误差的量化，误差可以按照不同的范数来衡量，如∞-范数（最大误差）、1-范数（误差绝对值之和）和2-范数（误差平方和的算术平方根）。其中，2-范数因其微分性质良好，常被选用于曲线拟合，因为它对应于误差能量的平方和，直观地反映了数据点到拟合曲线的整体偏差。 在实际操作中，对于给定的数据点集合{(x_i, y_i)}_{i=0}^{m}，在预先确定的函数类别（如多项式）中，我们寻找一个函数f(x)，使得所有数据点到该函数的垂直距离的平方和最小。这种寻找过程可以转化为求解多元函数的极值问题，通过多元函数的梯度等于零的条件得到一个线性方程组，即正规方程组或法方程组。对于多项式拟合，我们通常只考虑最高次幂不超过某个n的多项式，形成一个线性关系，例如： \[ \min_{\theta_0, \theta_1, ..., \theta_n} \sum_{i=0}^{m}(y_i - f(x_i))^2 \] 其中，\( f(x) = \theta_0 + \theta_1 x + ... + \theta_n x^n \)，而\( \theta_k \)们是待求的系数，\( k = 0, 1, ..., n \)。这个最小化问题等价于求解系数向量\( \theta \)使得满足正规方程组： \[ A\theta = b \] 其中\( A \)是对称正定矩阵，包含了数据点的信息，\( b \)是常数向量，\( A_{ij} = x_i^j \) 和 \( b_i = y_i \)。这个方程组确保了唯一解的存在，解出的\( \theta \)用于构建最小二乘拟合多项式。 拟合多项式的平方误差\( \sum_{i=0}^{m}(y_i - f(x_i))^2 \)被称为残差平方和，它是评估拟合效果的重要指标。通过最小化这个误差，我们得到的多项式能够最好地适应数据的分布趋势，从而实现对数据的近似。 总结来说，最小二乘法的核心思想是利用数学优化手段找到一组参数，使得数据点与拟合函数之间的误差平方和最小，这种方法在多项式拟合中尤为常见，且其求解过程涉及线性代数中的矩阵运算和特征，是理解统计建模和预测模型基础的重要组成部分。