理解数据结构：树与二叉树遍历

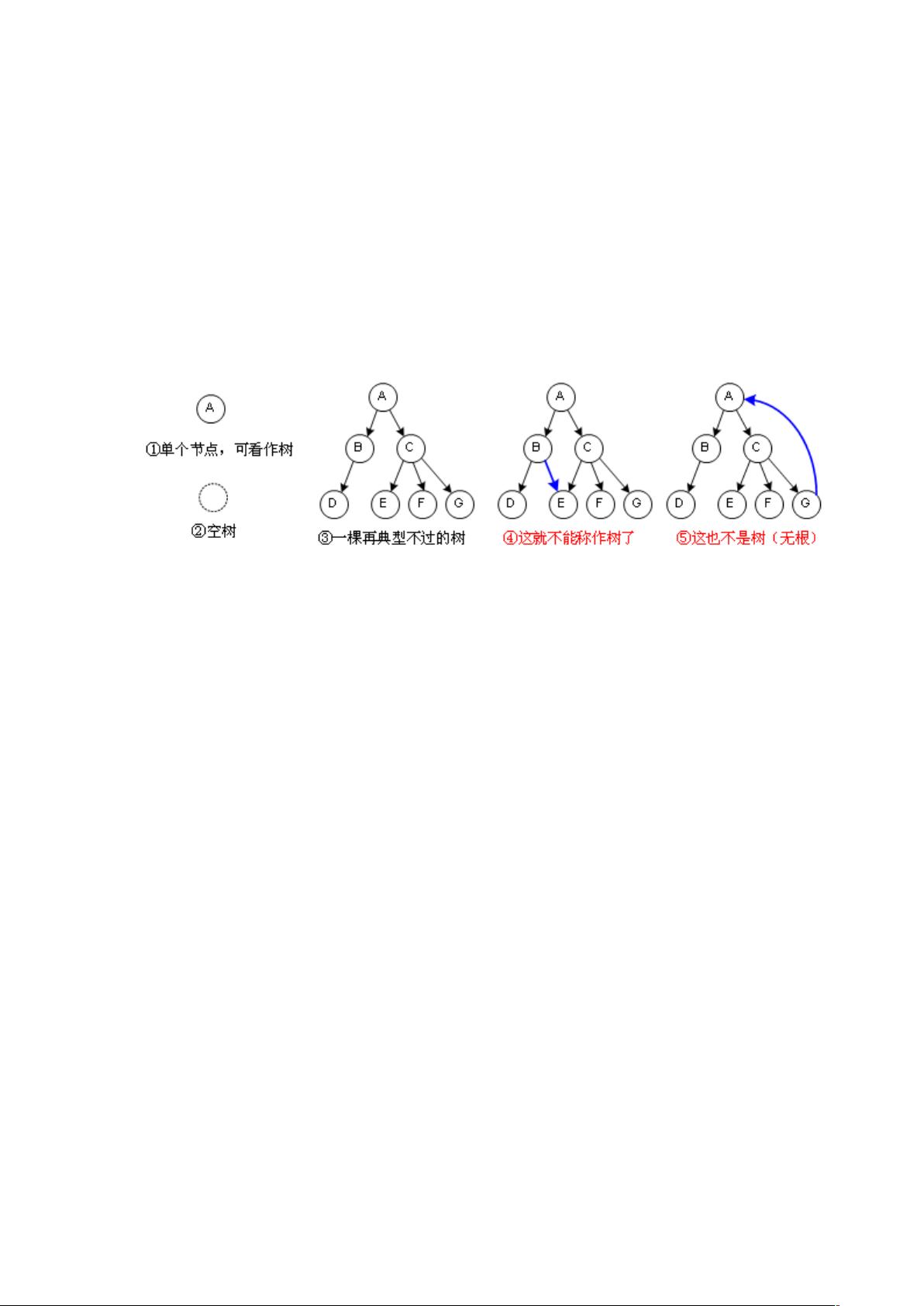
"这篇内容详细介绍了数据结构中的树和树的遍历，包括树的基本概念、二叉树的定义以及树的三种深度优先遍历方法。同时，文章提出了使用栈来实现二叉树的中序遍历，挑战非递归的方法。" 在计算机科学中，树是一种非常重要的数据结构，它由若干个节点组成，每个节点可以有零个或多个子节点。在树的结构中，有一个特殊的节点称为根节点，没有父节点，而没有子节点的节点被称为叶子节点。树的概念常用于表示层次关系或者组织结构，例如文件系统、网页链接等。 树的表示方式通常是以根节点在上，子节点在下的形式。在树中，节点之间的连接被称为边，而边的方向则决定了节点的父子关系。树的节点可以拥有任意数量的子节点，但二叉树是一个特殊类型的树，每个节点最多只有两个子节点，一个称为左子节点，另一个称为右子节点。 树的遍历是访问树中所有节点的过程，主要分为两种类型：广度优先遍历和深度优先遍历。广度优先遍历从根节点开始，按照层次顺序访问所有节点；深度优先遍历则是在树的分支上尽可能深地进行，有三种具体的方式：前序遍历、中序遍历和后序遍历。 - 前序遍历：先访问根节点，然后遍历左子树，最后遍历右子树。 - 后序遍历：先遍历左子树，然后遍历右子树，最后访问根节点。 - 中序遍历：对于二叉树，通常指的是左-根-右的顺序，即先遍历左子树，然后访问根节点，最后遍历右子树。这种方法在二叉搜索树中特别有用，因为它可以按顺序输出节点值。 在实际编程中，通常使用递归的方式来实现树的遍历，但递归可能会导致调用栈过深，特别是在处理大型树结构时。因此，使用栈来实现非递归的中序遍历是一个有效的替代方案。通过先将根节点的左子树压入栈中，然后不断弹出栈顶元素并访问，直到遇到叶子节点，接着访问当前节点，然后再将当前节点的右子树压入栈中，以此类推，可以实现中序遍历。 ```cpp #include <stack> using namespace std; class TreeNode { public: char val; TreeNode* left; TreeNode* right; TreeNode(char x) : val(x), left(NULL), right(NULL) {} ~TreeNode() {} }; void inorderTraversal(TreeNode* root) { stack<TreeNode*> s; TreeNode* curr = root; while (curr != NULL || !s.empty()) { while (curr != NULL) { s.push(curr); curr = curr->left; } curr = s.top(); s.pop(); // 访问当前节点 cout << curr->val << " "; curr = curr->right; } } ``` 以上代码展示了如何使用栈来实现非递归的中序遍历。通过不断地将左子节点压入栈，直到遇到叶子节点，然后弹出栈顶元素并访问，再转向其右子节点，可以保证中序遍历的顺序正确。这种方法不仅避免了递归带来的开销，也更容易理解和实现。