图解数据结构：图的概念与遍历

"图解考研数据结构_5_图.pdf" 本文将深入探讨图这一重要的数据结构，主要基于《图解考研数据结构》的部分内容。在计算机科学中，图是一种复杂的数据结构，由顶点（也称为节点）和边（连接顶点的关系）组成。它广泛应用于网络分析、算法设计、操作系统等多个领域。 首先，我们要理解图的基本概念。图分为无向图和有向图。无向图中的边没有方向，如图6-1(a)所示的G1，其中任意两个顶点之间可以互相连接；而有向图的边具有方向，如图6-1(b)所示的G2，边只能从一个顶点指向另一个顶点。图6-2展示了非简单图的示例，包括同一条边重复出现和顶点到自身的边，这在实际应用中可能需要特别处理。 接着，我们讨论子图的概念。如图6-4所示，子图是原图的一部分，包含原图中的部分顶点和它们之间的边。例如，图6-4(a)和(b)分别展示了无向图G1和G2的子图。 对于连通性，无向图的连通性是判断图是否可以从任一顶点到达其他所有顶点的关键。图6-5展示了连通图和非连通图以及连通分量的概念。连通图如G1，所有的顶点都可以通过边相连；非连通图G3则包含多个不相交的连通分量，如图6-5(b)和(c)所示。 强连通图是特殊的有向图，其中任意两个不同的顶点之间都存在双向的路径。图6-6解释了强连通图与非强连通图的差异，并展示了强连通分量，即图中每个顶点都可以通过边到达其他所有顶点的子图。 生成树是无向图的一种子集，包含了所有顶点且边形成一棵树形结构，没有环路。图6-7展示了连通图G5及其生成树，而图6-8则阐述了非连通图G6及其生成森林，即每个连通分量的生成树的集合。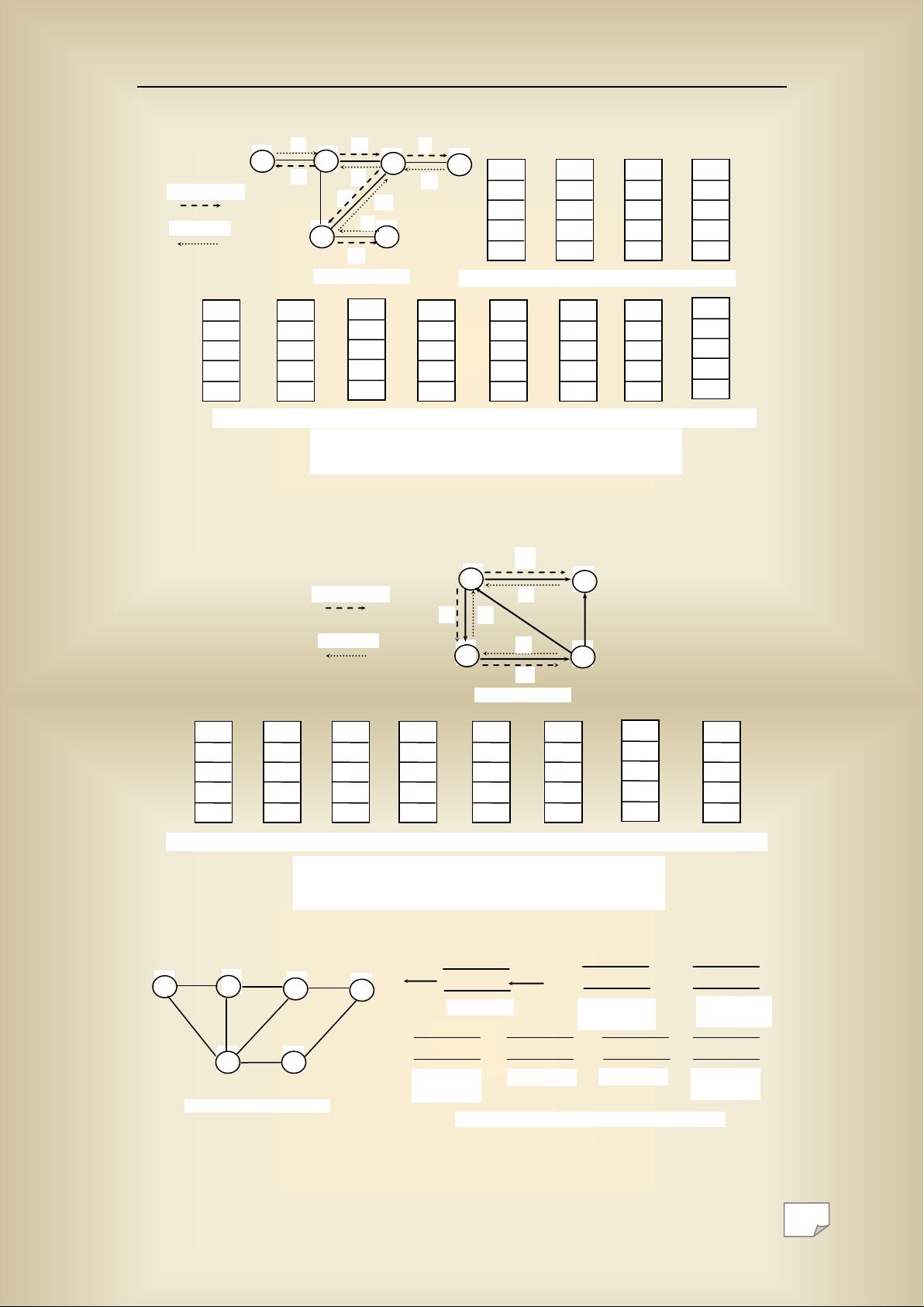 接下来，我们关注深度优先遍历（DFS）。DFS是一种遍历或搜索图的方法，从一个顶点开始，沿着边向下探索，直到访问完所有可达的顶点。图6-9和6-10展示了无向图和有向图的DFS过程，通过栈来记录遍历路径。DFS常用于检测环路、查找连通性和构建生成树等。 最后，广度优先遍历（BFS）是从一个顶点开始，先访问其相邻顶点，再依次访问这些相邻顶点的相邻顶点。虽然文中未直接展示BFS，但它在寻找最短路径、层次遍历等问题中扮演重要角色。 总结来说，图是数据结构中的核心概念，理解其基本类型、子图、连通性、强连通性、生成树以及遍历方法对解决各种计算机科学问题至关重要，尤其是在考研复习和实际编程中。掌握这些知识能够帮助我们设计出更高效、更实用的算法。