"马踏棋盘算法实现与思路梳理"
需积分: 0 162 浏览量
更新于2023-12-19
1
收藏 414KB DOCX 举报
"数据结构之马踏棋盘具体算法实现"
本文将详细讨论数据结构中马踏棋盘问题的具体算法实现。通过以下目录来展开讨论:
1. 问题引出
2. 理清思路
3. 柳暗花明
3.1 如何表示马可以走的坐标
### 1. 问题引出
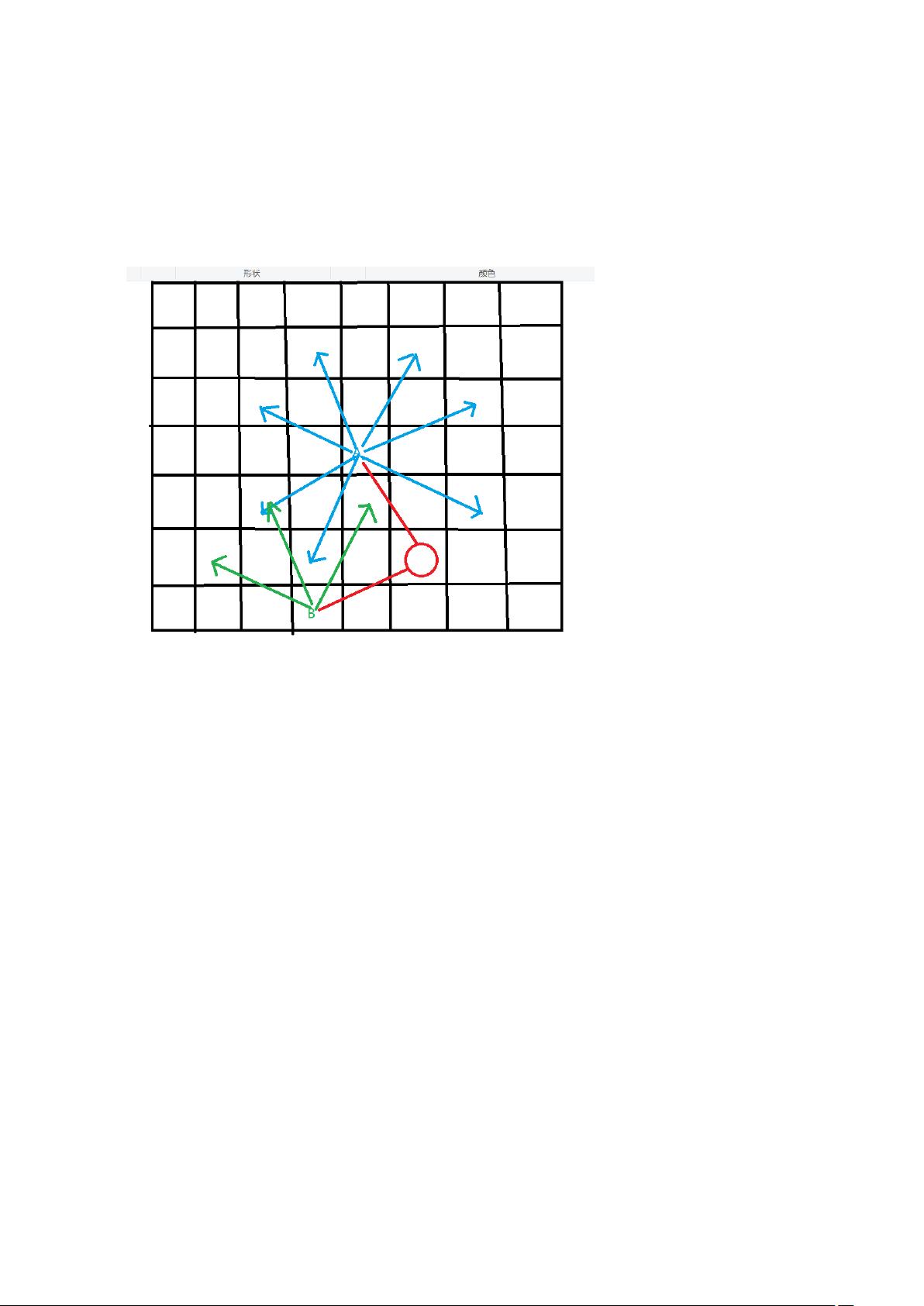
马踏棋盘问题是一个经典的数学和计算机科学问题。在象棋中,马可以走“日”字形的步伐,即每走一步可以横向或纵向移动一个格子,然后再向左或向右移动两个格子,或者横向或纵向移动两个格子,然后再向上或向下移动一个格子。这个问题要求在一个给定的棋盘上,马从任意一个起点出发,经过每一个格子恰好一次,最终回到起点。这个问题有时也被称为“骑士周游问题”。
### 2. 理清思路
为了解决马踏棋盘问题,我们需要使用适当的数据结构和算法。一种常见的方法是使用回溯算法,通过不断试探和回溯来寻找解决方案。在这个过程中,我们需要维护一个棋盘的状态,记录每个格子是否已经被访问过,并且尝试不同的移动方式来找到可行的路径。在实际编码中,我们可以使用二维数组来表示棋盘状态,使用递归函数来实现回溯算法,以及使用一些辅助数据结构来帮助实现算法。
另外,我们还可以优化算法,使用一些启发式策略来减少搜索空间,以提高解决问题的效率。例如,可以通过预先计算每个格子可行的移动路径,来避免不必要的遍历,从而减少搜索的时间复杂度。
### 3. 柳暗花明
在实际编码中,我们可以首先定义一个二维数组来表示棋盘状态,使用0表示未访问的格子,使用1表示已访问的格子。然后,我们可以编写一个递归函数来实现马踏棋盘的回溯算法。在每一步中,我们需要考虑马当前的位置和可行的移动方式,然后尝试每一种移动方式,直到找到解决方案或者无法继续移动为止。如果找到解决方案,我们就可以输出路径;如果无法继续移动,则需要回溯到上一步,尝试其他的移动方式。
同时,我们还可以使用一些启发式策略来优化算法。例如,我们可以预先计算每个格子可以走的下一步可行走的路径的数量,然后按照这个数量的大小来进行排序,优先尝试可行路径数较小的格子,这样可以避免一些不必要的搜索,提高算法效率。
综上所述,通过合理的数据结构和算法设计,我们可以很好地解决马踏棋盘问题,并且可以通过一些优化策略来提高算法的效率。马踏棋盘问题是一个非常经典的问题,通过对这个问题的研究和实践,我们可以锻炼自己的编程能力和解决问题的思维能力。希望本文的内容能够对读者有所帮助,同时也欢迎读者们进行讨论和分享,共同进步。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2012-06-29 上传
2015-10-08 上传
2015-07-29 上传
2011-12-08 上传
点击了解资源详情
2013-10-24 上传
苏嵌老咸鱼
- 粉丝: 0
- 资源: 1