黄河小浪底调水调沙：Matlab拟合曲线分析

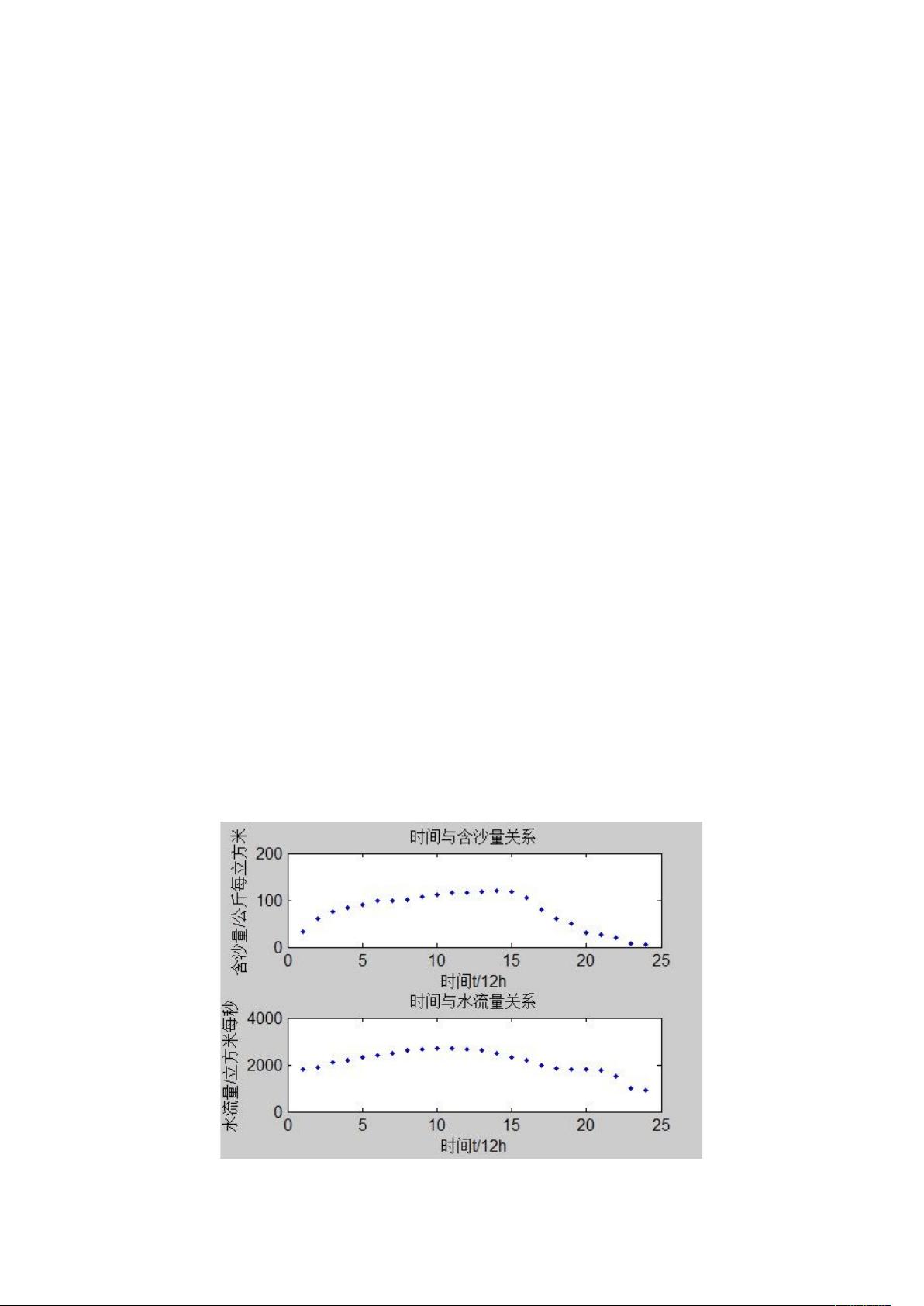
"黄河小浪底调水调沙问题是运用数学建模和Matlab进行拟合曲线分析的一个实例。此问题关注的是通过水利工程调控来清除水库中的泥沙，特别是小浪底、三门峡和万家寨三大水库的联合调度。在2004年的试验中，小浪底水库在6月19日至7月13日进行了预泄放水，以形成人造洪峰冲刷沉积的泥沙。观测数据显示了不同时间点的水流量和含沙量，为建立数学模型提供了基础数据。模型的构建旨在估算任意时刻的排沙量及总排沙量，并确定排沙量与水流量之间的关系。" 在这个问题中，关键知识点包括： 1. **数学建模**：数学建模是一种用数学语言描述现实世界现象的过程，它能帮助我们理解和预测复杂系统的行为。在这里，模型需要考虑水流量和含沙量随时间的变化，以估计排沙量。 2. **Matlab**：Matlab是一款强大的数值计算和数据分析软件，常用于处理和分析数据，建立和求解数学模型。在这个案例中，可以使用Matlab进行数据拟合，找出水流量和含沙量之间的函数关系，以及它们与排沙量的关联。 3. **拟合曲线**：拟合曲线是数学建模中的一个重要步骤，目的是找到一个数学函数来最佳地描述观测数据。在黄河小浪底问题中，可能需要使用线性、多项式或指数等函数来拟合水流量和含沙量的数据，以便进一步分析。 4. **小浪底调沙**：小浪底水利枢纽是黄河上的重要工程，其调水调沙策略是通过控制水流量来清除沉积的泥沙，以保持水库的正常运行。在这个过程中，理解水流量与含沙量的动态关系至关重要。 5. **数据处理**：对观测到的水流量和含沙量数据进行整理和分析是解决问题的关键。这可能涉及到数据清洗、时间序列分析和统计建模等方法。 6. **连续函数假设**：在模型构建中，假设水流量和含沙量是连续变化的，这简化了问题并允许使用微积分方法来计算排沙量。每个12小时的观测点被视为时间点t，通过这些点可以近似整个时间段内的变化趋势。 7. **关系确定**：通过数据分析和拟合，可以确定排沙量V与水流量v(t)和含沙量S(t)之间的关系，例如V = v(t)S(t)。这个关系可以帮助预测不同条件下的排沙效果，并为未来的调水调沙策略提供理论依据。 在实际操作中，可能还需要考虑其他因素，如气候影响、泥沙颗粒大小分布、水力条件等，但基于给定的数据和假设，主要目标是建立一个简化的模型来揭示基本的物理过程，并提供排沙策略的初步评估。