数值方法在自然科学中的应用

"这是一份关于计算方法的讲义，主要针对自然科学研究第一部分B的课程，由剑桥大学应用数学与理论物理系的Stuart Dalziel教授编写。讲义内容涵盖1999年 Lent Term的教学内容，包含了完整的讲座笔记，并提供了多种格式和可见性的选项，包括子节、子子节、第四级子节、全文本、公共方程式（在手册中完整给出）、隐藏方程式（在手册中不完整）以及全部图形和表格。此外，还涉及了课程目标、推荐书籍、编程、工具（如软件库和数学系统）以及课程学分和版本信息。" 本文将深入探讨计算方法这一主题，它在自然科学领域中扮演着至关重要的角色，因为它允许科学家和工程师处理无法通过解析方法解决的复杂问题。计算方法是数值分析的一个分支，它涉及到一系列算法和技术，用于近似地求解数学问题，尤其是那些在实际中遇到的非线性问题、偏微分方程或大型线性代数问题。 1. **课程目标**：计算方法的主要目标是教给学生如何使用计算机来解决科学和工程中的数学问题，这些问题是无法通过封闭形式的解析解来解决的。这通常包括学习如何设计和分析数值算法，以确保它们的稳定性和精度。 2. **书籍推荐**：对于学习计算方法，推荐的通用书籍可能包括经典的数值分析教材，如Richard L. Burden 和 J. Douglas Faires的《数值分析》或Gene H. Golub 和 Charles F. Van Loan的《矩阵计算》。此外，还有一些更专门的书籍，可能专注于特定的计算方法或应用领域。 3. **编程**：掌握至少一种编程语言是必要的，因为计算方法的实施往往需要编程。Python、Matlab、Fortran 和 C++ 是常见的选择，它们都有强大的科学计算库支持。 4. **工具**：软件库如Numpy和SciPy为Python提供了广泛的数值计算功能，而MATLAB则是一个广泛使用的数学计算环境，内置了丰富的数值算法。更高级的数学系统，如Maple和Mathematica，提供了符号计算能力，也可以进行数值计算。 5. **课程学分**：完成这门课程可能会获得一定的学分，具体取决于所在学校的课程设置。 6. **版本信息**：讲义可能有多个版本，每个版本可能根据教学需求有不同的格式和内容显示。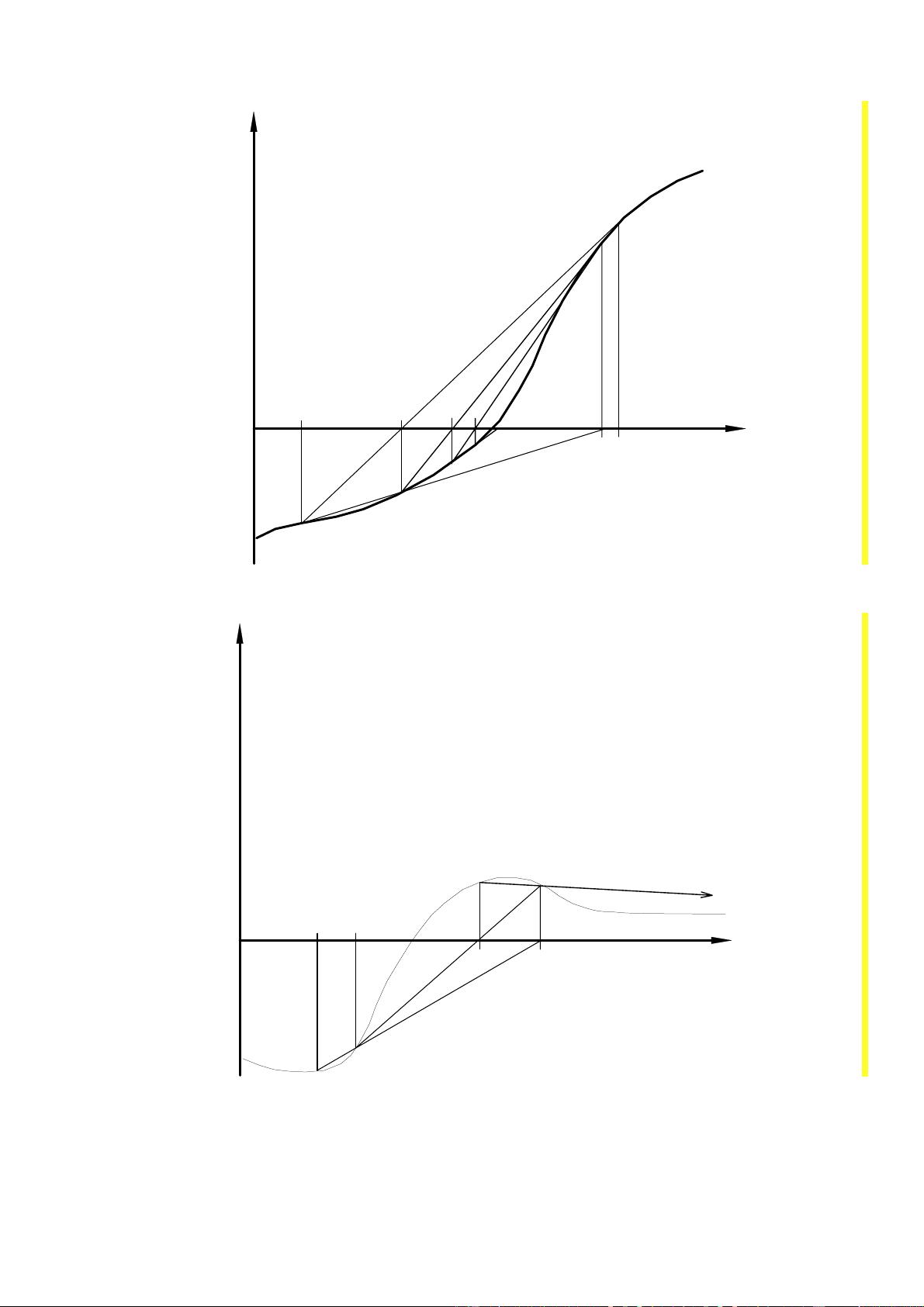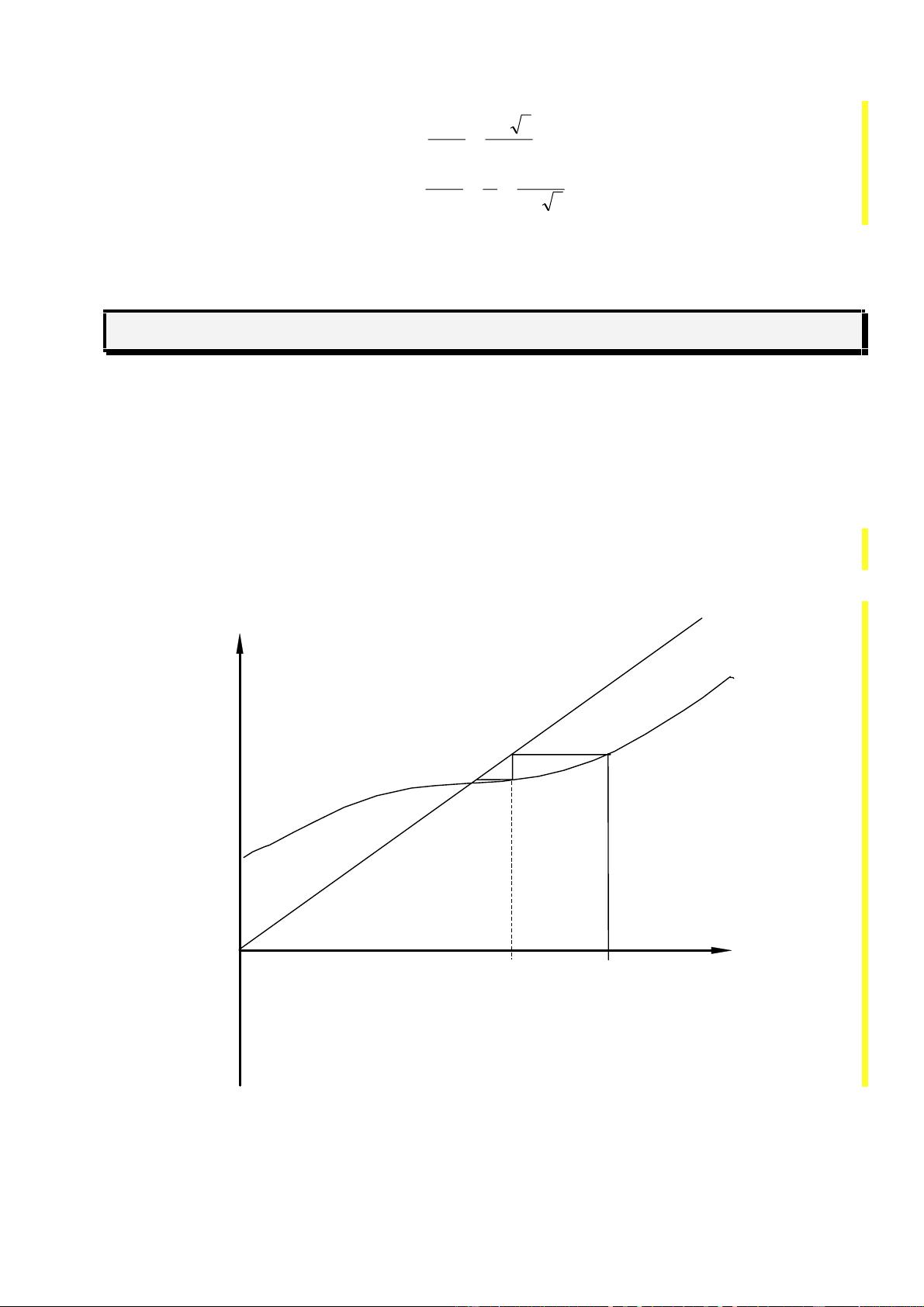 这份讲义将详细讲解各种计算方法，如插值、数值积分、微分方程的数值解、优化问题以及线性代数问题的数值解法。学生将通过学习这些方法，获得解决实际问题的能力，这对于自然科学和工程领域的研究和实践至关重要。