线性规划优化图像增强技术

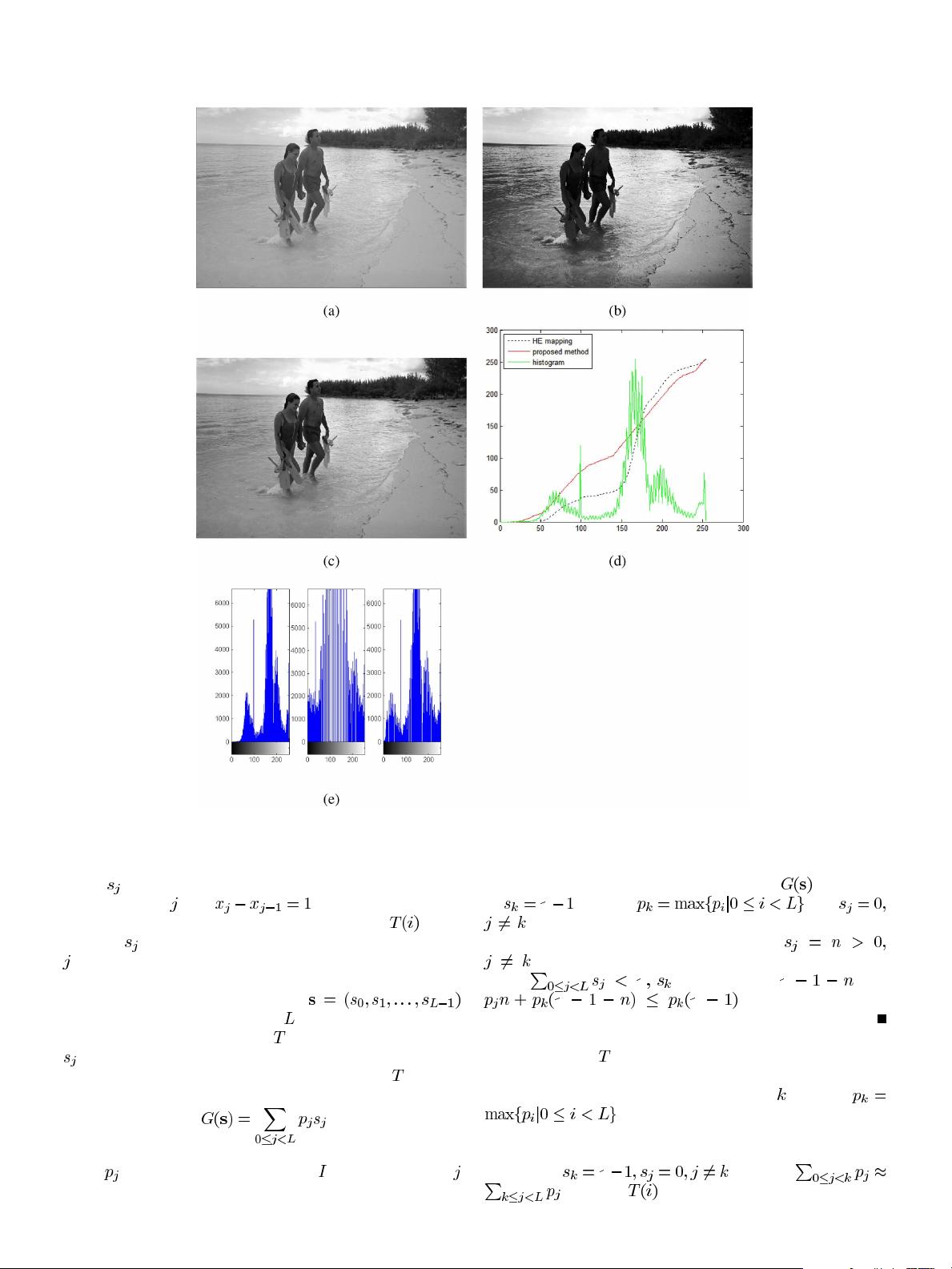
"线性规划在图像增强中的应用" 线性规划是一种优化技术，通常用于解决在满足一组线性约束条件下，最大化或最小化一个线性目标函数的问题。在图像处理领域，线性规划被用来实现一种新颖的图像增强算法，即通过最优对比度色调映射来提升图像质量。这种方法与传统的直方图均衡化方法不同，它不是简单地调整像素的直方图分布，而是以最大化预期对比度增益为目标，同时限制色调失真在一个可接受的范围内，并可选择性地添加其他约束以避免图像增强过程中可能出现的失真或伪影。 具体来说，线性规划在这里的作用是找到最佳的映射函数，该函数能将图像的原始像素值映射到新的值，以达到增强对比度的效果，同时控制色调失真不超过预设阈值。这一过程可以通过构建一个线性优化模型来实现，模型的目标函数是对比度增益，约束条件包括色调失真限制和其他可能的用户自定义约束。由于线性规划问题可以高效求解，因此这种方法在实际应用中具有较高的计算效率。 线性规划优化的图像增强方法具有一定的通用性，用户可以根据需要添加和微调约束条件，以达到理想的视觉效果。例如，可以限制局部区域的亮度变化，或者保证某些颜色通道的保真度，以保留图像的关键特征。实验结果显示，这种新方法相对于传统的直方图均衡化及其变种，能够显著提升图像增强的性能，提供更清晰、更自然的视觉体验。 关键词：对比度增强，动态范围，直方图均衡化，线性规划，色调再现。 在实际应用中，线性规划图像增强可能涉及以下几个关键步骤： 1. 图像预处理：对原始图像进行必要的预处理，如去除噪声、校正色彩偏差等。 2. 建立优化模型：根据增强目标和约束条件构建线性规划模型，包括定义目标函数（对比度增益）和约束条件（如色调失真限制）。 3. 求解线性规划：利用现有的线性规划求解器（如Simplex算法或内点法）寻找最佳映射函数。 4. 像素映射：将原始图像的像素值按照求得的最佳映射函数进行转换。 5. 后处理：可能需要进行一些后处理操作，如平滑过渡、消除边界效应等，以获得更加平滑和自然的增强图像。 这种方法的优势在于，它不仅提高了图像的对比度，还能有效控制图像的色调变化，减少可能产生的不自然效果，使得图像增强后的结果更接近人眼的感知，从而在视觉上提供更好的体验。此外，由于线性规划的灵活性，用户可以根据不同的应用场景和需求调整约束条件，使得增强效果更具针对性。