信息论基础：哈工大贾世楼研究生课程讲义解析

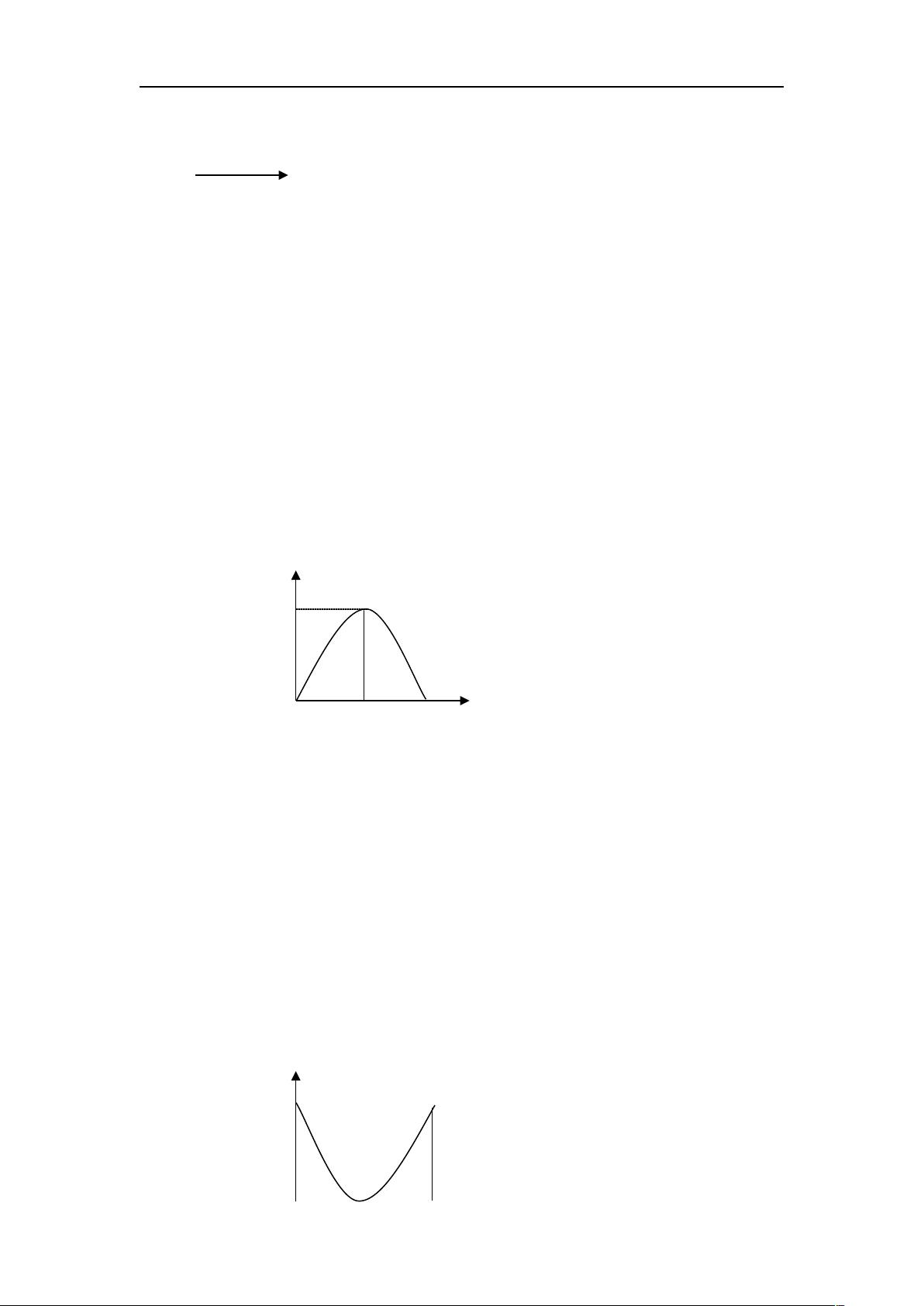
"哈尔滨工业大学贾世楼教授的信息论研究生课程讲义，主要探讨了第二章中的平均交互信息量I(X,Y)的相关特性。" 在信息论中，平均交互信息量I(X,Y)是一个核心概念，它衡量的是信源X与信宿Y之间的信息关联程度。在统计平均的意义下，它描述了信源、信道和信宿组成的通信系统的信息传输效率。I(X,Y)的非负性是一个重要的性质，表明在任何情况下，信源与信宿之间至少存在正向的信息传递。 平均交互信息量I(X,Y)的非负性可以通过对数的上凸性来证明。如果f(x)是一个上凸函数，如f(x)=logx，那么对于概率分布π，有f(∑πixi)≥∑πif(xi)。应用这个性质到I(X,Y)，我们可以推导出I(X,Y)≥0。只有当X和Y完全独立，即P(X,Y)=P(X)P(Y)，平均交互信息量I(X,Y)才会等于零。这意味着，接收者在收到Y的符号时，总能从Y中获取关于X的信息，除非X和Y完全独立。 平均交互信息量的另一个关键特性是它的互易性，即I(X,Y)=I(Y,X)。这表示Y中关于X的信息量与X中关于Y的信息量是相等的。这种互易性反映了信息传递的双向性，尽管观察角度可能不同，但从X到Y和从Y到X的信息量是等价的。通过信息熵的差异，可以表示为I(X,Y)=H(X)-H(X/Y)=H(Y)-H(Y/X)，其中H(X/Y)和H(Y/X)分别是条件熵，表示在已知Y的情况下X的熵和在已知X的情况下Y的熵。 此外，当X和Y独立时，联合熵H(X,Y)等于它们各自的熵之和，即H(X,Y)=H(X)+H(Y)，同时条件熵H(X/Y)=H(X)且H(Y/X)=H(Y)，这意味着在没有相互依赖的情况下，从一方获取的信息不会增加另一方的不确定性。 在信息传输过程中，后验熵H(X/Y)总是小于或等于先验熵H(X)，这是后熵不增加原理，确保信息处理不会凭空增加信息。同样，H(Y/X)≤H(Y)也反映了这一原则。这些原理是信息理论中的基本定律，对理解和优化通信系统的性能至关重要。 图示部分可能展示了I(X,Y)如何作为两个随机变量分布的重叠部分，直观地解释了X和Y之间的信息共享程度。平均交互信息量I(X,Y)就是这种共享信息的量化度量。 哈尔滨工业大学的这份信息论课程讲义深入探讨了平均交互信息量的非负性、互易性和其在通信系统中的实际意义，这些都是理解和应用信息理论不可或缺的基础知识。