最小二乘法在系统辨识中的精确应用与验证

最小二乘法在系统辨识中的应用是基于最优化算法的一种关键技术，它在控制领域的系统分析与建模中发挥着重要作用。系统辨识是通过收集实际系统的输入输出数据，推断出反映系统动态特性的数学模型，而最小二乘法正是这种过程中的核心工具。本文聚焦于将最小二乘法应用于水压仿真器的系统辨识，这是一种电液压力伺服系统，它的性能对控制精度有直接影响。 首先，通过线性最小二乘问题的介绍，阐述了最小二乘法的基本原理。线性最小二乘法假设系统的动态关系是线性的，通过最小化预测值与实际值之间的误差平方和（损失函数），找到最佳拟合模型。这个过程依赖于矩阵运算，如残差矩阵和雅可比矩阵，通过求解这些矩阵的逆或特征值问题，确定模型参数。 对于非线性最小二乘问题，尽管实际系统可能并非完全线性，但最小二乘法可以通过迭代优化方法近似处理，例如梯度下降法或牛顿法，逐步调整模型参数以降低误差。文献中采用的是递推最小二乘算法，这是一种适合在线或实时应用的非线性辨识方法，它在处理复杂系统时展现出良好的鲁棒性和效率。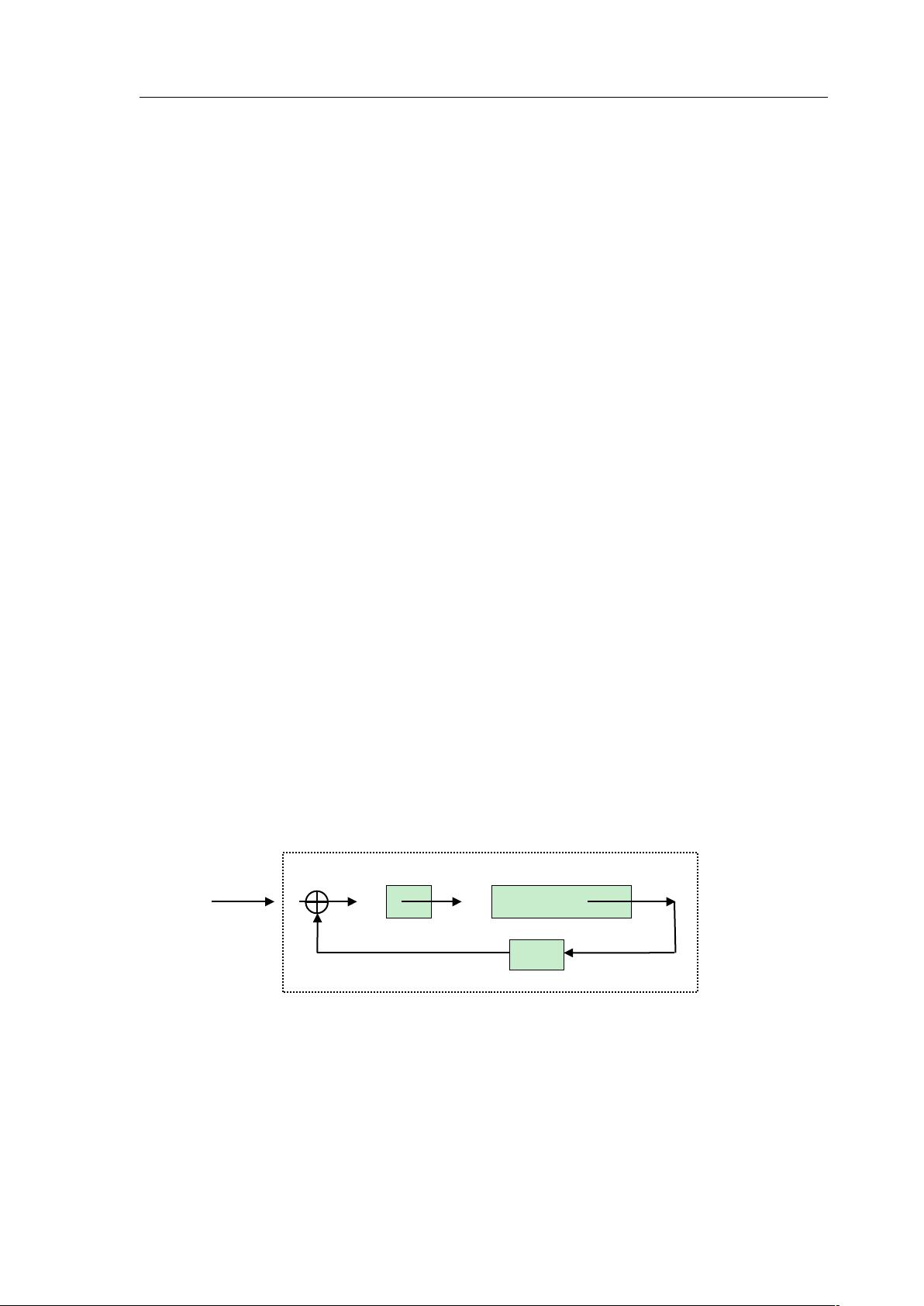 在水压仿真器的实际应用中，通过设计稳定的闭环控制系统，输入不同的信号，如伪随机序列，记录输出，然后利用最小二乘算法对数据进行拟合，得出辨识模型。模型的准确性体现在其阶跃响应曲线能较好地匹配实际系统的响应，这表明辨识结果有效并且接近真实系统的行为。 然而，系统辨识并非完美无缺，辨识结果总会存在一定程度的误差，因为无法精确捕捉到所有的非线性行为和噪声影响。因此，文中强调了辨识结果是以某种特定准则为基础的，这种准则可能包括模型的复杂度、计算效率和精度的权衡。 总结来说，最小二乘法在系统辨识中的应用体现了其在最优化问题求解中的强大能力，特别是在处理控制系统的动态特性识别时，通过不断优化模型参数，提供了可靠的数据驱动方法。通过实际案例——水压仿真器的研究，展示了最小二乘法如何帮助工程师理解并控制复杂系统的行为，从而为实际工程设计和控制策略提供依据。