RS码入门详解：从概念到伽罗瓦域运算

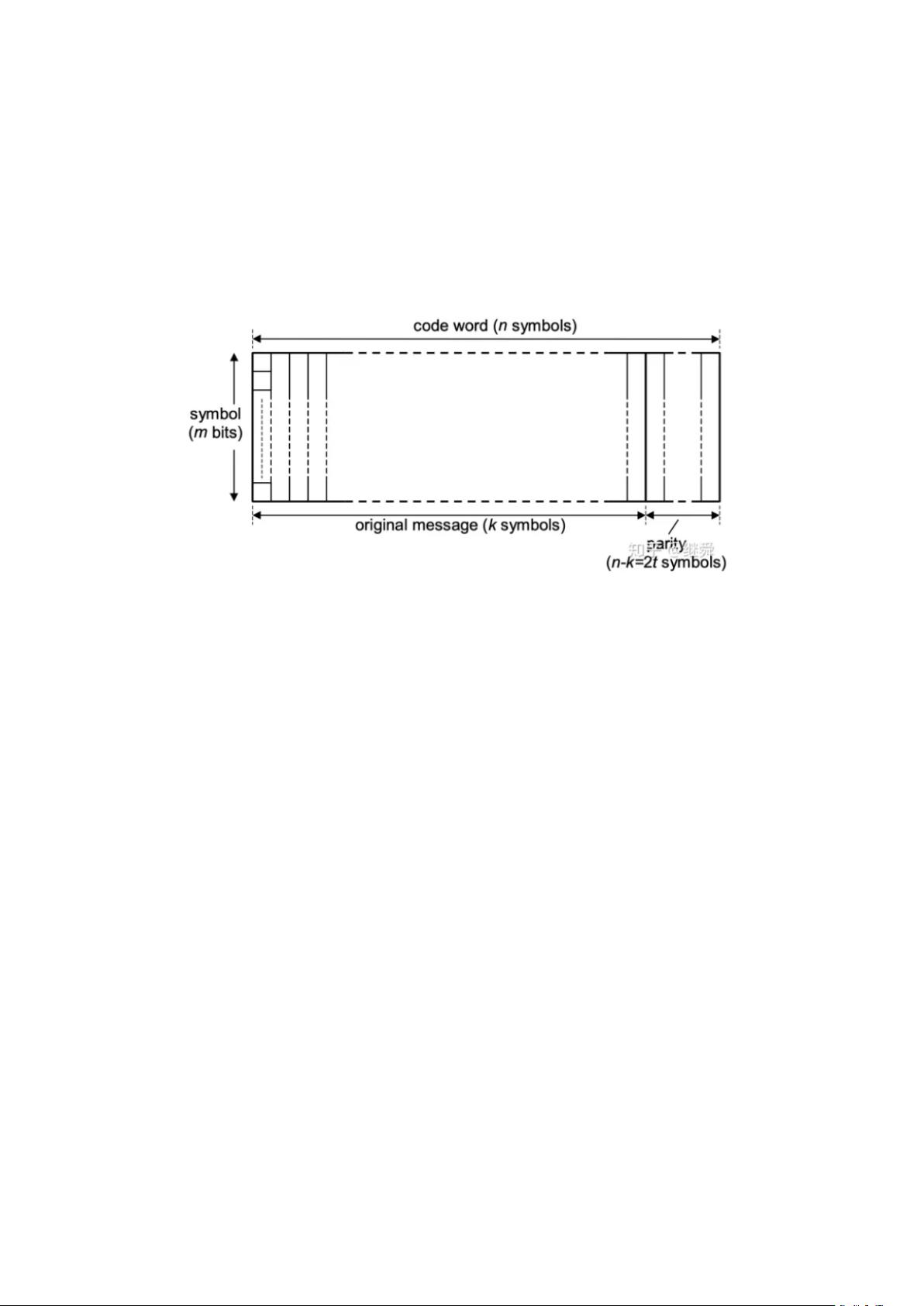
"RS码0基础理解，浅显易懂 - ReedSolomon 纠错码" Reed-Solomon (RS)码是一种强大的纠错编码技术，主要用于纠正数据传输或存储过程中可能出现的错误。这种编码方法是由麻省理工学院的Reed和Solomon在1960年提出，适用于多种场景，如CD、DVD、蓝光光盘的纠错、卫星通信、网络传输等。 1. RS码的基本概念 RS码通过添加额外的校验信息来增强数据的抗错误能力。在RS(n,k)码中，"n"是总码字数量，"k"是信息码字数量，而"t"是可纠正的错误数量。因此，"n-k"是用于纠错的校验码字数量，通常表示为2t，这意味着RS码可以纠正最多"t"个错误码字（每个码字通常由多个比特，即symbol组成，常见的symbol大小为8位）。 2. 伽罗瓦域（Galois Field） RS码的理论基础是伽罗瓦域，这是一个有限的数学结构，其中的运算遵循特定的规则。例如，GF(2^m)代表一个包含2的m次幂个元素的伽罗瓦域。在这个域中，加法和减法是相同的，与异或操作等价。伽罗瓦域中的运算并不遵循自然数域的常规算术规则。 2.1 伽罗瓦域的生成 本原多项式在伽罗瓦域中扮演关键角色，它生成该域的所有非零元素。例如，在GF(2^4)，一个本原多项式可能是P(x) = x^4 + x + 1，通过不断乘以x并取模P(x)，可以生成所有16个元素，包括0和1。 2.2 伽罗瓦域内的运算 - 加减法：在GF(2^m)中，加法和减法是按位异或操作，具有交换性和结合性。 - 乘法：乘法遵循多项式规则，超出域范围的项需要取模。乘法运算满足交换律、结合律和分配律。 - 除法：寻找一个元素的逆元进行除法，即找到一个元素乘以分母后等于1的元素。在GF(2^m)中，每个非零元素都有一个逆元，并且除法运算同样满足结合律和分配律。 3. RS码的生成与解码 - 生成：RS码的生成涉及将信息码字扩展为更大的码字序列，通过伽罗瓦域内的运算添加校验信息。 - 解码：当接收到带有错误的码字时，RS码的解码算法（如贝斯-索洛蒙算法或范德蒙特矩阵方法）能够检测并纠正错误，恢复原始信息。 RS码的高效性和纠错能力使其成为现代通信和数据存储系统中的关键技术。尽管这里只介绍了基本概念，但深入理解RS码需要对代数、线性代数和编码理论有更深入的了解。