"最大公约数与最小公倍数-C程序设计谭浩强"

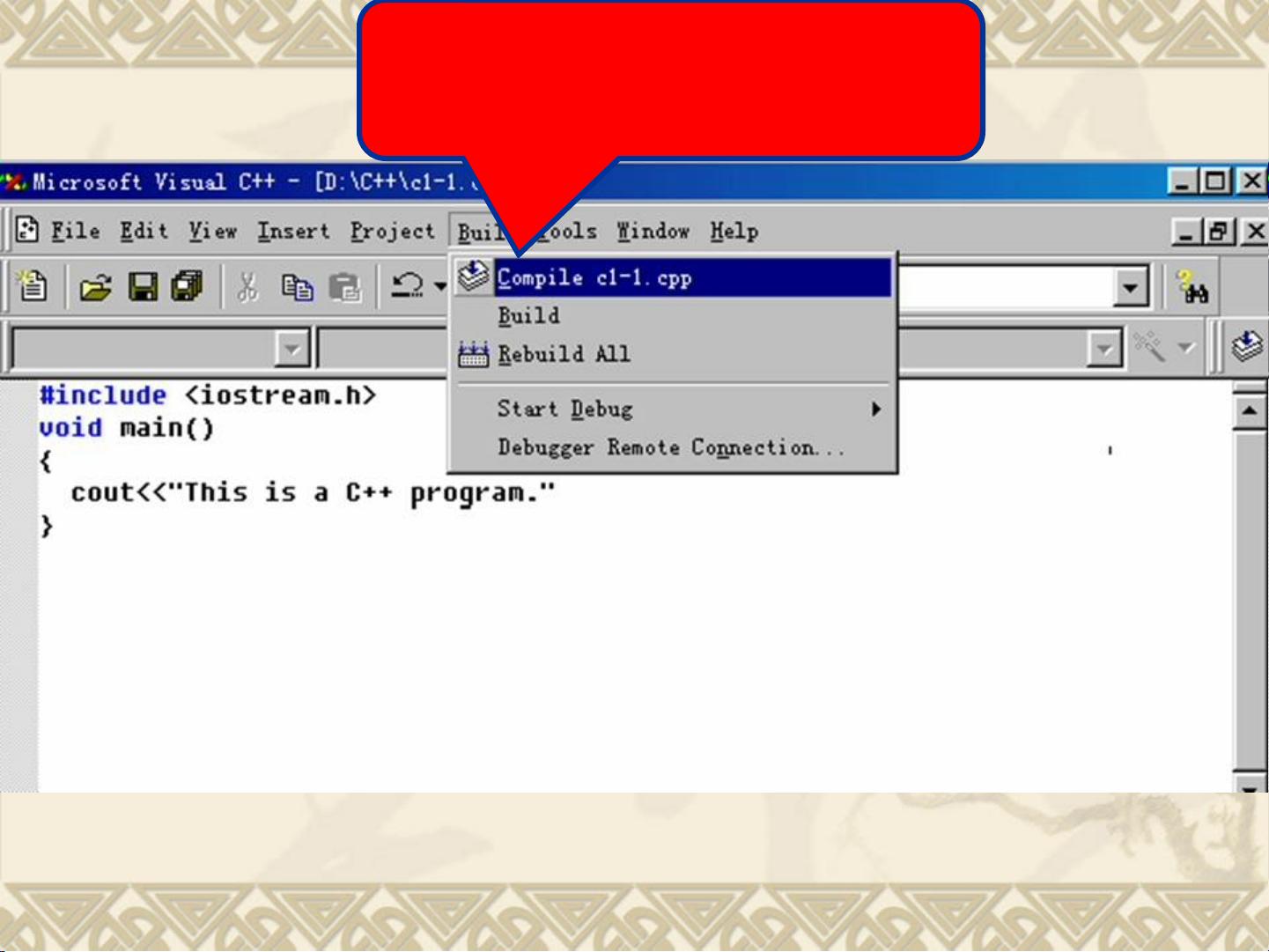
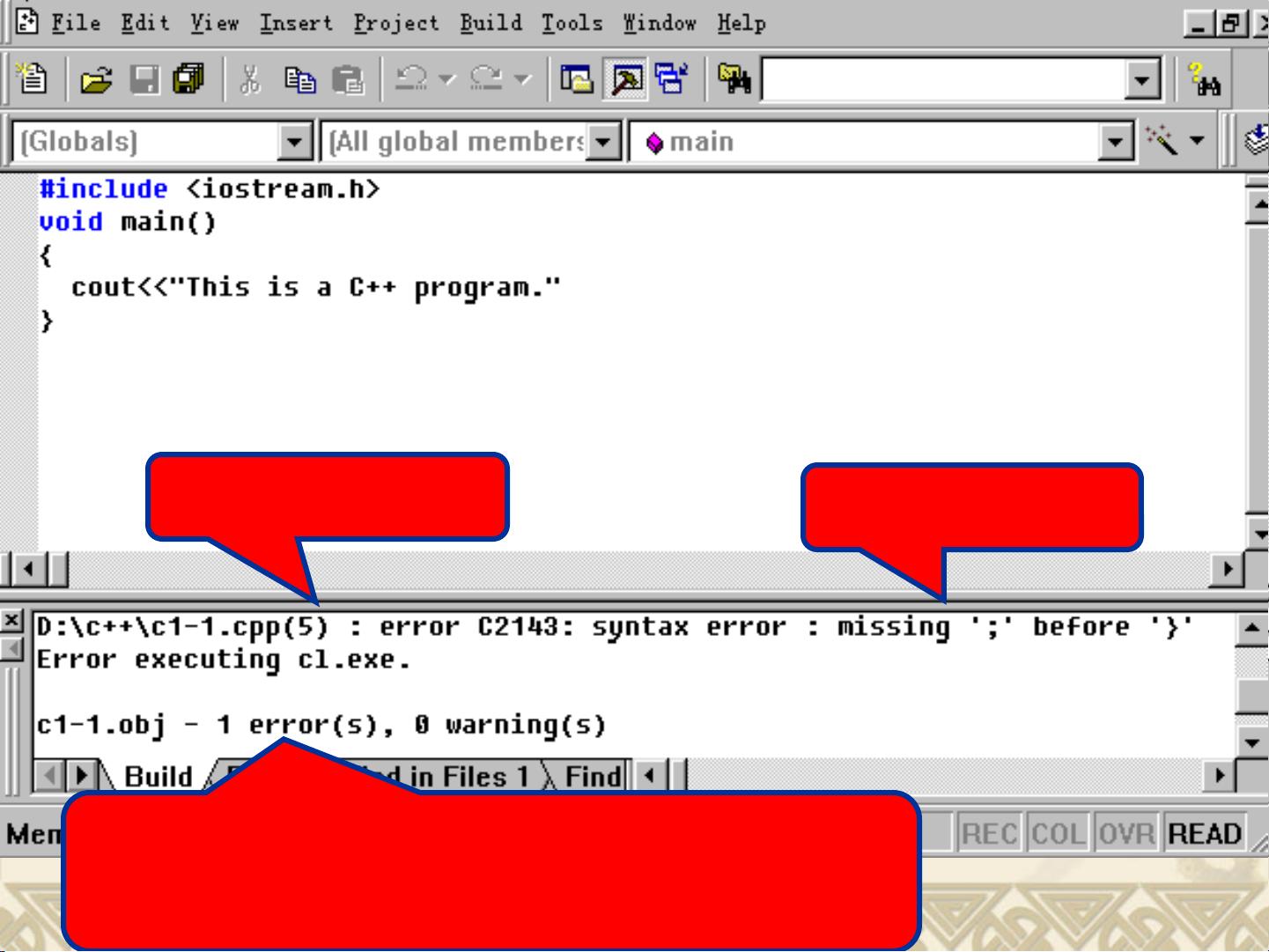
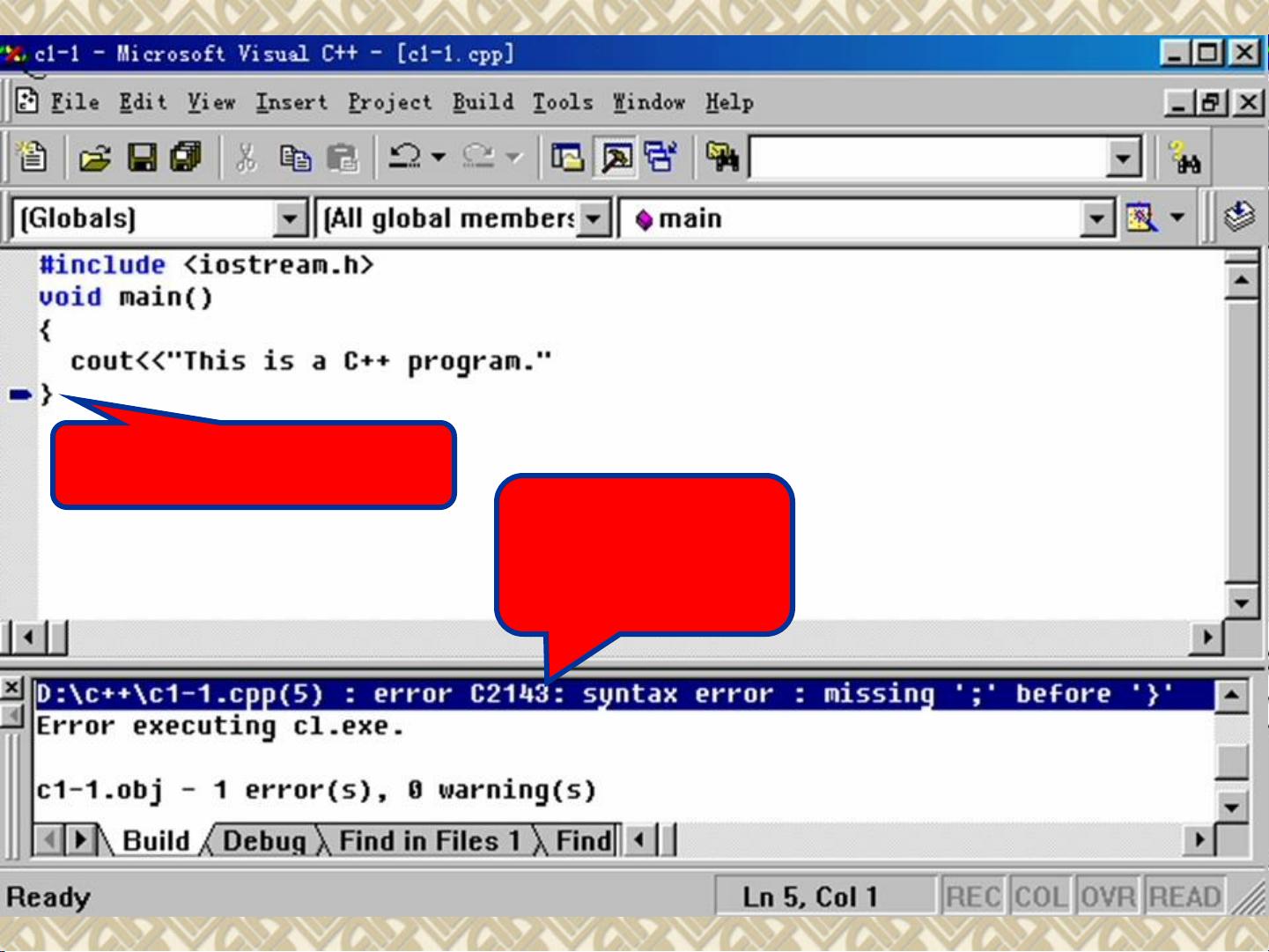
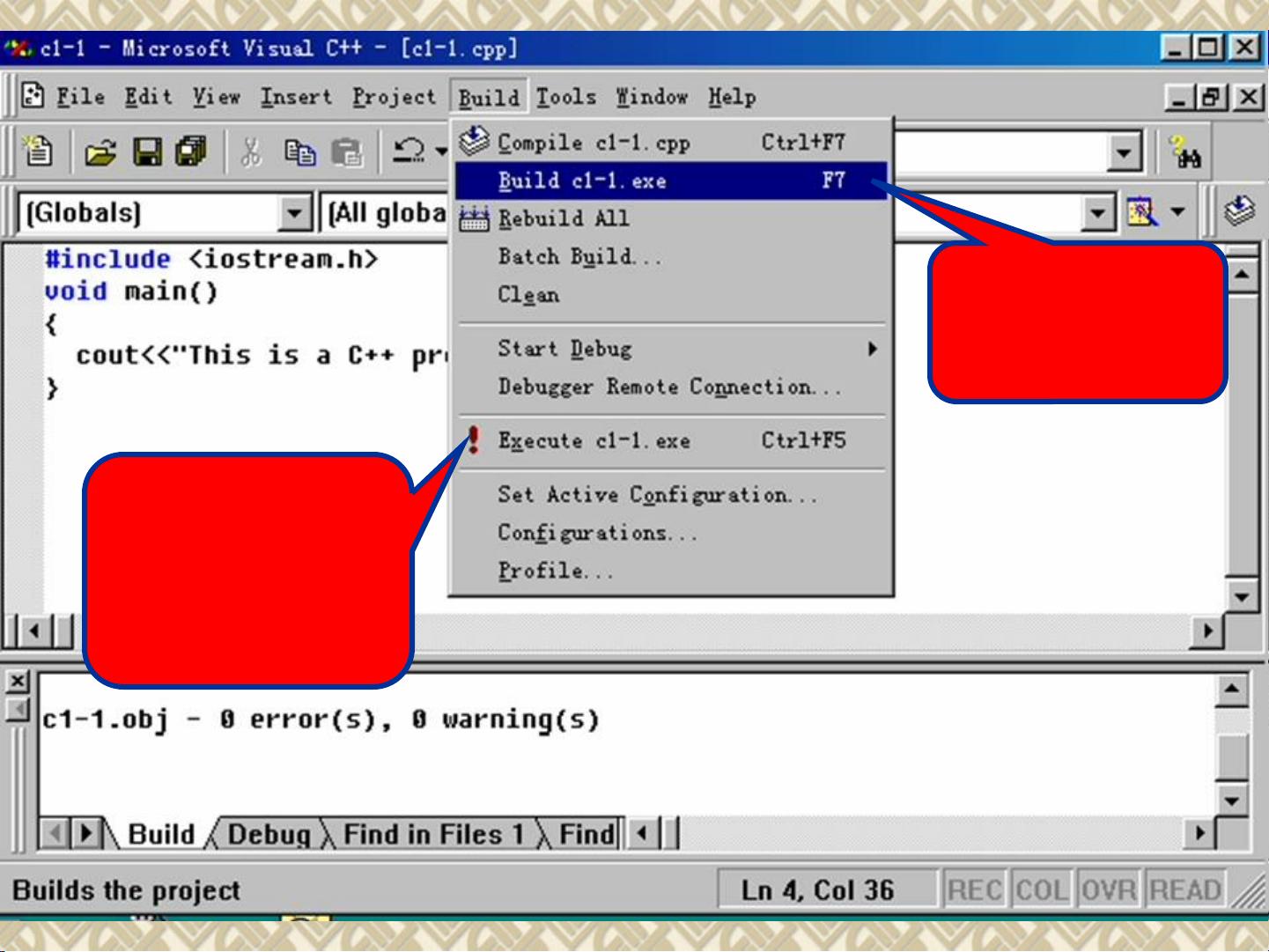
最大公约数与最小公倍数是数学中常见的概念，计算两个数的最大公约数和最小公倍数可以通过欧几里德算法来实现。当给定两个自然数m和n时，首先求得它们的余数r，然后通过循环计算直至余数为0，此时较小的数即为最大公约数。而最小公倍数则可以通过两数之积除以最大公约数得到。C语言是一种常用的程序设计语言，有着悠久的历史和不断更新的发展。从BCPL语言到B语言，再到贝尔实验室的Dennis Ritchie和Brian Kernighan在此基础上发明的C语言，每一次的改进都使得程序设计更加高效。随着计算机技术的飞速发展，C语言在各种应用领域中发挥着重要作用，也为程序设计带来了更多的可能性。 欧几里德算法在计算最大公约数时体现了简洁而高效的思想，通过不断求取余数和更新两个数的值，最终可以得到它们的最大公约数。这一算法的实现过程可以用循环结构来描述，使得计算过程清晰明了。而在求得最大公约数后，我们可以通过两数之积除以最大公约数得到最小公倍数，这种关联的计算过程可以更好地理解数学中最大公约数和最小公倍数的概念。 C语言作为一种高效的程序设计语言，其发展历程也体现了计算机软件领域的不断创新和衍生。从最早的BCPL语言到B语言再到C语言，每一代的语言都在前一代的基础上进行改进和完善，使得程序设计更具灵活性和实用性。贝尔实验室的Dennis Ritchie和Brian Kernighan在B语言的基础上发展出的C语言更是成为了当今广泛应用的程序设计语言之一，其简洁而功能强大的特点使得其在各种领域都有着广泛的应用。 总的来说，最大公约数与最小公倍数的计算以及C语言作为程序设计语言的发展历程都是计算机科学领域中的重要内容。通过欧几里德算法可以求得两个数的最大公约数，从而掌握了一种简单而高效的数学计算方法。而C语言作为一种高效的程序设计语言，其不断更新换代的发展历程为计算机软件领域带来了更多的可能性，使得程序设计变得更加便捷高效。最终，数学与计算机科学的结合为人们在日常生活和工作中带来了更多的便利和效率。