"概率论与数理统计公式全解析：排列组合、加法和乘法原理、随机事件及其概率"

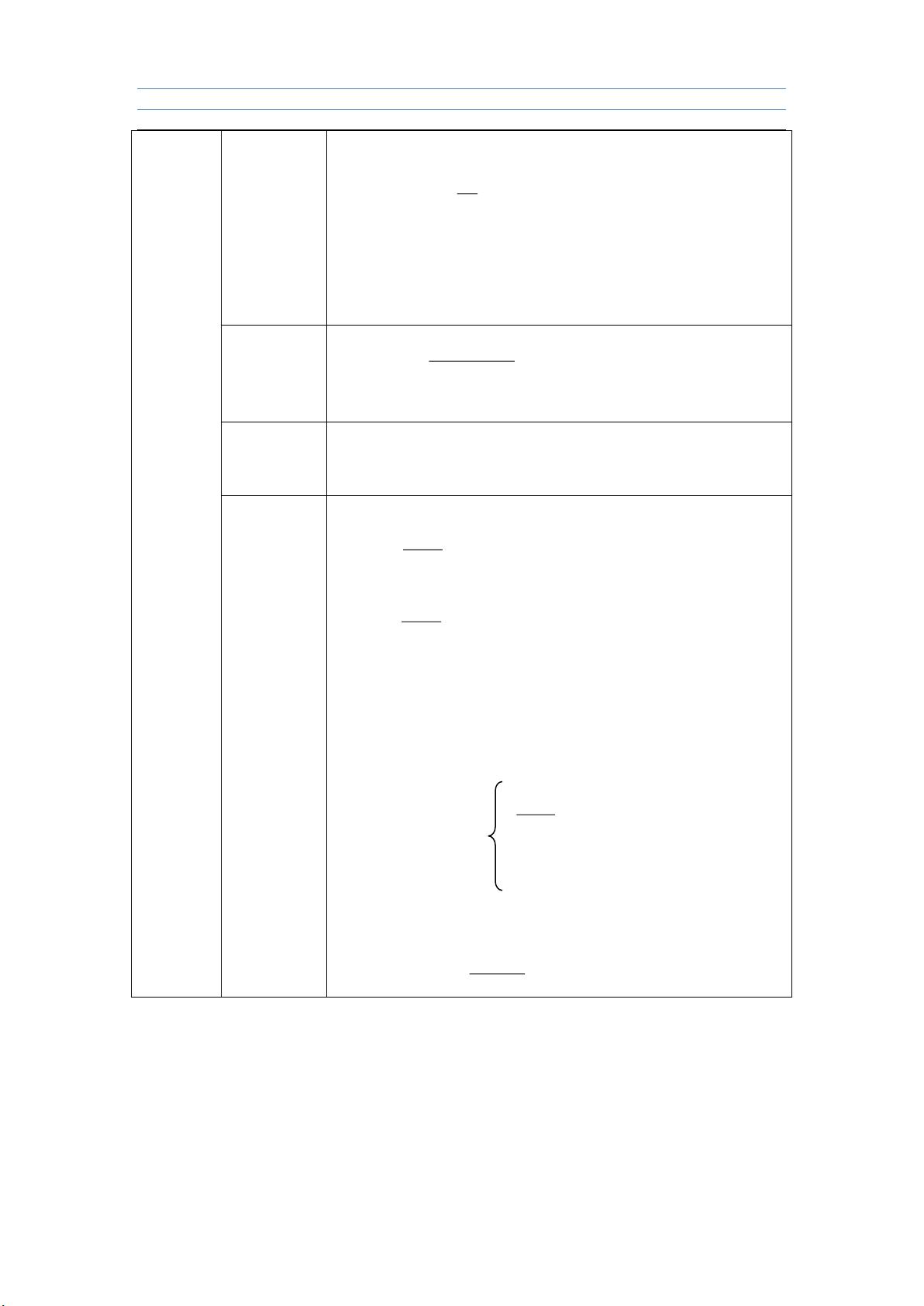
概率论与数理统计是一门研究随机现象规律性的学科，其中包含了大量复杂的公式和理论。在第一章中，我们学习了关于随机事件及其概率的理论与公式。其中包括排列组合公式，加法和乘法原理，一些常见排列，随机试验和随机事件，基本事件、样本空间和事件等内容。 排列组合公式是概率论与数理统计中重要的一部分。从 m 个人中挑出 n 个人进行排列的可能数的计算公式为 mPn = m!/(m-n)!，而从 m 个人中挑出 n 个人进行组合的可能数的计算公式为 mCn = m!/(n!*(m-n)!)。这些公式在实际问题中有着广泛的应用，能够帮助我们计算出不同的可能性。 此外，加法和乘法原理也是概率论与数理统计中的重要内容。加法原理指的是当某件事由两种方法来完成时，这件事可由这两种方法的乘积种方法来完成。而乘法原理指的是当某件事由两个步骤来完成时，这件事可由这两个步骤的乘积种方法来完成。这两个原理在实际问题中有着广泛的应用，能够帮助我们解决复杂的计算问题。 在随机事件方面，我们学习了一些常见排列包括重复排列和非重复排列，对立事件（至少有一个），顺序问题等内容。此外，我们还学习了随机试验和随机事件的概念。随机试验是指在相同条件下可以重复进行的试验，而每次试验的可能结果不止一个，但在进行一次试验之前却不能断言它出现哪个结果。试验的可能结果称为随机事件。这些概念在实际问题中帮助我们对随机现象有更深入的理解，从而能够进行概率的计算和分析。 最后，我们学习了基本事件、样本空间和事件的概念。在一个试验下，不管事件有多少个，总可以从中找到一些基本事件，它们构成了样本空间。而事件则是样本空间的子集，表示了一些基本事件的组合。这些概念能够帮助我们更清晰地理解随机事件的可能性，并且在概率的计算中起到重要作用。 总的来说，概率论与数理统计的第一章内容涵盖了许多重要的公式和理论，它们为我们理解和分析随机现象提供了重要的工具和方法。通过学习这些内容，我们能够掌握如何计算不同的可能性和概率，更好地理解随机事件的规律性，为实际问题的分析和应用提供了重要的理论基础。