Java实现二叉搜索树:查找、插入、删除与遍历解析
198 浏览量
更新于2024-09-02
收藏 108KB PDF 举报
"Java 实现二叉搜索树的查找、插入、删除、遍历"
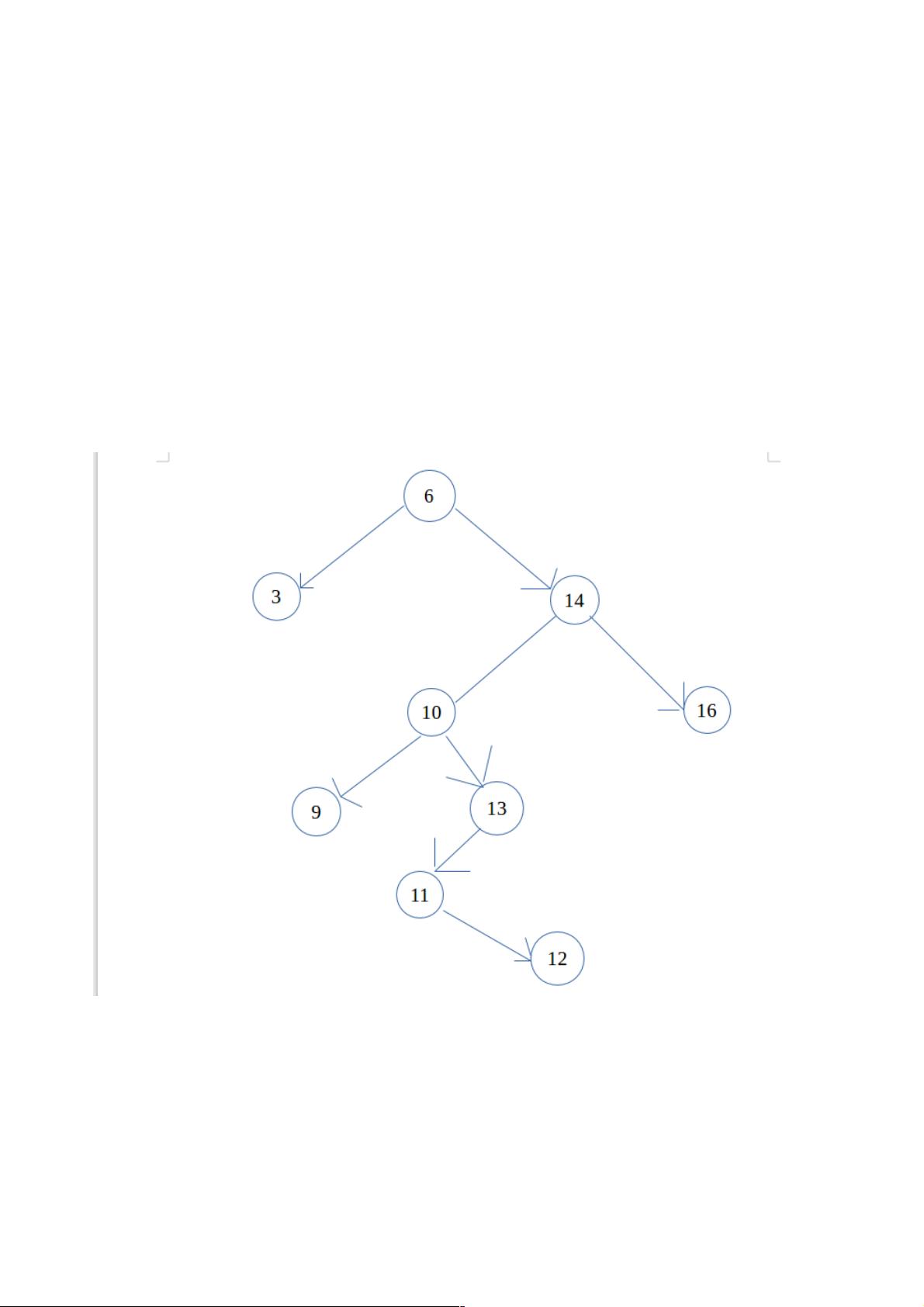
二叉搜索树(Binary Search Tree,简称BST),是一种特殊的二叉树数据结构,它具有以下特性:
1. 每个节点包含一个键(key)、一个关联的值、一个指向左孩子的指针和一个指向右孩子的指针。
2. 节点的键大于其左子树中的任何节点的键。
3. 节点的键小于其右子树中的任何节点的键。
4. 左子树和右子树也必须是二叉搜索树。
5. 不存在键相同的节点。
基于这些特性,二叉搜索树提供了一种高效的数据组织方式,使得查找、插入和删除操作的时间复杂度可以达到O(log n)的理想情况,但在最坏情况下(树退化成链表)则会变为O(n)。
在Java中实现二叉搜索树,首先需要定义一个Node类来表示树的节点,如下所示:
```java
class Node {
int key;
int value;
Node leftChild;
Node rightChild;
public Node(int key, int value) {
this.key = key;
this.value = value;
}
public void displayNode() {
// 显示节点的键和值
}
}
```
接着,定义一个Tree类来维护整个二叉搜索树:
```java
class Tree {
Node root; // 保存树的根
// 查找指定节点
public Node find(int key) {
// 实现查找逻辑
}
// 插入节点
public void insert(int key, int value) {
// 实现插入逻辑
}
// 删除指定节点
public boolean delete(int key) {
// 实现删除逻辑,可能需要找到待删除节点的直接后继节点
Node directPostNode = getDirectPostNode(delNode);
// ...
}
// 得到待删除节点的直接后继节点
private Node getDirectPostNode(Node delNode) {
// 实现逻辑
}
// 先序遍历树
public void preOrder(Node rootNode) {
// 实现先序遍历逻辑:根-左-右
}
// 中序遍历树
public void inOrder(Node rootNode) {
// 实现中序遍历逻辑:左-根-右
}
// 后序遍历树
public void postOrder(Node rootNode) {
// 实现后序遍历逻辑:左-右-根
}
}
```
在上述代码中,`find()`方法用于查找具有特定键的节点,`insert()`方法用于插入新的键值对,`delete()`方法负责删除指定键的节点。`getDirectPostNode()`方法在删除操作中用来找到待删除节点的直接后继节点,以保持树的性质。最后,`preOrder()`, `inOrder()`, 和 `postOrder()`方法分别实现了先序、中序和后序遍历,它们是二叉树常用的三种遍历策略。
在查找操作中,从根节点开始,如果目标键等于当前节点的键,则返回当前节点;如果目标键小于当前节点的键,就向左子树递归查找;如果目标键大于当前节点的键,就向右子树递归查找。插入操作类似,找到合适的位置创建新节点。删除操作通常分为三种情况:无子节点、一个子节点和两个子节点,每种情况下的处理方式都不同,需要考虑到如何保持树的平衡。
遍历操作则按照特定顺序访问每个节点。先序遍历顺序为根-左-右,中序遍历顺序为左-根-右,后序遍历顺序为左-右-根。这些遍历方法在数据处理、打印树结构或计算树的属性时非常有用。
在实际应用中,为了优化二叉搜索树,可以考虑使用自平衡树,如AVL树或红黑树,它们在插入和删除操作后能自动调整,以保持树的平衡,从而确保操作的效率。例如,JDK 1.8中的HashMap在负载因子达到一定程度时会转为红黑树,以提高哈希表在高并发场景下的性能。
点击了解资源详情
点击了解资源详情
点击了解资源详情
点击了解资源详情
2024-10-26 上传
2020-12-21 上传
2021-05-08 上传
点击了解资源详情
点击了解资源详情
weixin_38672840
- 粉丝: 9
- 资源: 893
最新资源
- MATLAB实现小波阈值去噪:Visushrink硬软算法对比
- 易语言实现画板图像缩放功能教程
- 大模型推荐系统: 优化算法与模型压缩技术
- Stancy: 静态文件驱动的简单RESTful API与前端框架集成
- 掌握Java全文搜索:深入Apache Lucene开源系统
- 19计应19田超的Python7-1试题整理
- 易语言实现多线程网络时间同步源码解析
- 人工智能大模型学习与实践指南
- 掌握Markdown:从基础到高级技巧解析
- JS-PizzaStore: JS应用程序模拟披萨递送服务
- CAMV开源XML编辑器:编辑、验证、设计及架构工具集
- 医学免疫学情景化自动生成考题系统
- 易语言实现多语言界面编程教程
- MATLAB实现16种回归算法在数据挖掘中的应用
- ***内容构建指南:深入HTML与LaTeX
- Python实现维基百科“历史上的今天”数据抓取教程