应用数学统计：连续与离散分布概览

"Mathematical Statistics with Applications" 是一本关于数理统计的英文教材，涵盖了概率分布、矩生成函数、期望值与方差等核心概念。 在统计学中，概率分布是描述随机变量可能取值及其概率的重要工具。以下是部分连续和离散分布及其关键属性的概述： 1. **均匀分布 (Uniform Distribution)**： - 定义：如果一个随机变量Y服从区间[θ1, θ2]上的均匀分布，其概率密度函数（PDF）为 f(y) = 1/(θ2 - θ1)，其中θ1 ≤ y ≤ θ2。 - 均值 (Mean)：θ1 + θ2 / 2 - 方差 (Variance)：(θ2 - θ1)^2 / 12 2. **正态分布 (Normal Distribution)**： - 公式：f(y) = 1 / (σ * √2π) * exp[-(y - µ)^2 / (2σ^2)]，其中y位于-∞到+∞之间，μ是均值，σ是标准差。 - 矩生成函数 (Moment-Generating Function, MGF)：M(t) = exp[µt + σ^2t^2 / 2] 3. **指数分布 (Exponential Distribution)**： - PDF：f(y) = 1/β * e^(-y/β)，其中y > 0，β > 0是率参数。 - 均值与方差：均值 = β，方差 = β^2 4. **伽马分布 (Gamma Distribution)**： - PDF：f(y) = 1 / (Γ(α) * β^α) * y^(α-1) * e^(-y/β)，其中y > 0，α和β是形状参数。 - MGF：M(t) = (1 - βt)^(-α) 5. **卡方分布 (Chi-square Distribution)**： - PDF：f(y) = (y^(v/2 - 1)) / (2^(v/2) * Γ(v/2)) * e^(-y/2)，其中y > 0，v是自由度。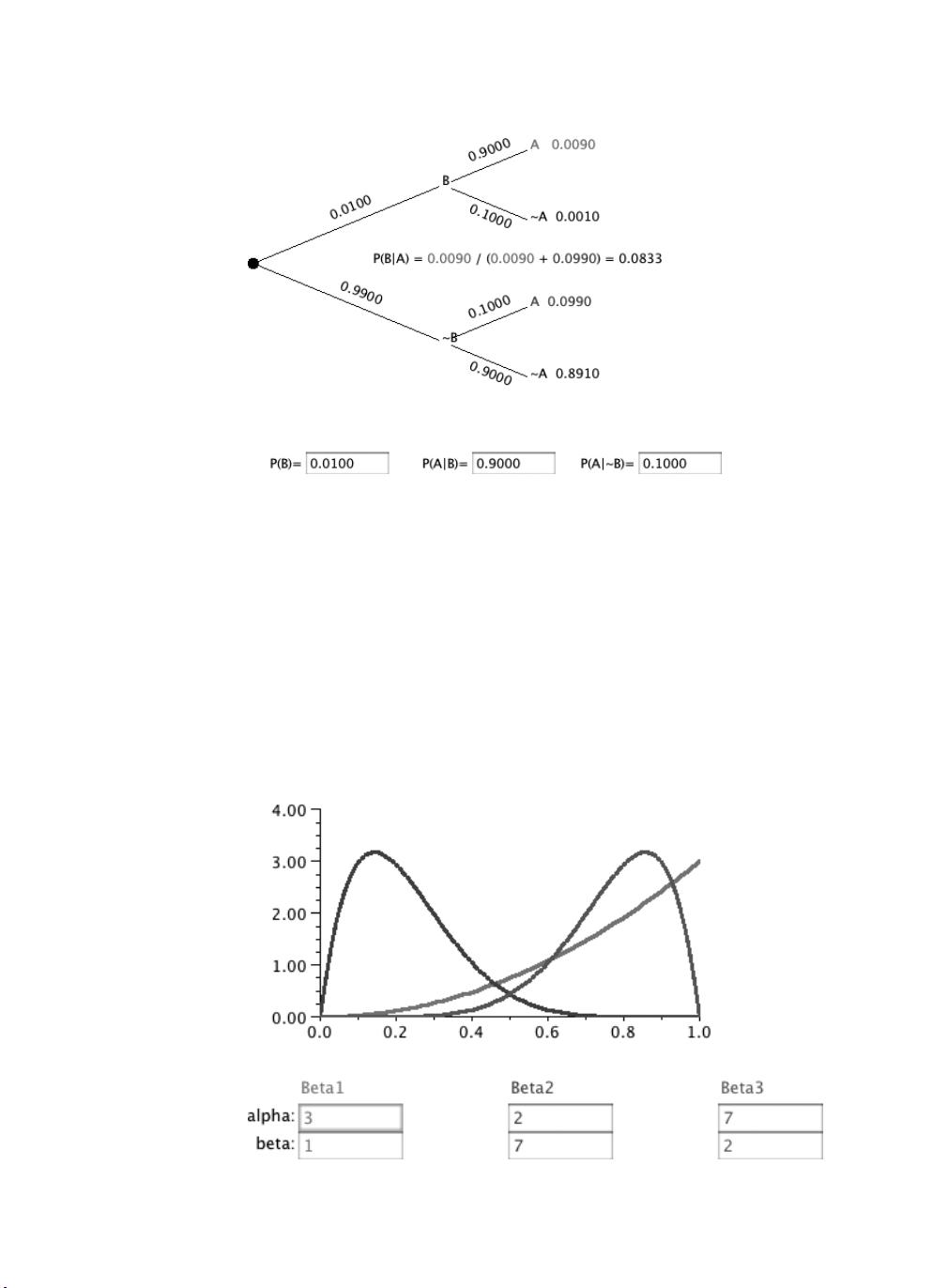 - MGF：M(t) = (1 - 2t)^(-v/2) 6. **贝塔分布 (Beta Distribution)**： - PDF：f(y) = Γ(α + β) / (Γ(α) * Γ(β)) * y^(α-1) * (1-y)^(β-1)，其中0 < y < 1，α和β是形状参数。 - 由于没有封闭形式的矩生成函数，通常需要数值方法来计算。 对于离散分布，包括二项分布、几何分布、超几何分布、泊松分布和负二项分布，它们的特点如下： 1. **二项分布 (Binomial Distribution)**： - 概率质量函数 (PMF)：p(y) = C(n, y) * p^y * (1-p)^(n-y)，其中y = 0, 1, ..., n，n是试验次数，p是每次试验成功的概率。 - 均值与方差：均值=np，方差=np(1-p) 2. **几何分布 (Geometric Distribution)**： - PMF：p(y) = p * (1-p)^(y-1)，其中y = 1, 2, ...，p是每次试验成功的概率。 - 均值与方差：均值=1/p，方差=1/p^2 3. **超几何分布 (Hypergeometric Distribution)**： - PMF：p(y) = C(r, y) * C(N-r, n-y) / C(N, n)，其中r是成功状态的总数，N是总体大小，n是抽取样本的大小。 - 无矩生成函数的封闭形式表达 4. **泊松分布 (Poisson Distribution)**： - PMF：p(y) = λ^y / y! * e^(-λ)，其中y = 0, 1, 2, ...，λ是事件发生的平均速率。 - 均值与方差：均值=λ，方差=λ 5. **负二项分布 (Negative Binomial Distribution)**： - PMF：p(y) = C(y-1, r-1) * p^r * (1-p)^(y-r)，其中y = r, r+1, ...，r是成功前的失败次数。 - 均值与方差：均值=r/p，方差=r*p/(1-p) 这些概率分布是数理统计中基础且重要的工具，用于描述各种随机现象，并在假设检验、参数估计和置信区间的构建等方面发挥关键作用。了解并掌握这些分布的性质对于进行统计分析至关重要。