Python实现朴素贝叶斯分类：概率与决策理论详解

朴素贝叶斯是一种基于概率论的简单但强大的分类方法，它属于贝叶斯分类算法的一种。该方法的核心概念源自贝叶斯定理，该定理阐述了在给定某些证据或特征的情况下，我们如何更新对某个事件发生的概率估计。朴素贝叶斯算法之所以被称为“朴素”，是因为它假设特征之间相互独立，尽管在现实世界中这种假设往往并不成立，但在许多实际问题中，它仍然表现良好。 在Python编程中，朴素贝叶斯算法常用于文本分类、垃圾邮件过滤、情感分析等领域，因为它的计算速度快且对数据量要求相对较低。算法的工作流程如下： 1. 贝叶斯定理基础: - 贝叶斯定理描述了在给定一些条件的情况下，一个事件发生概率与这些条件出现概率之间的关系。形式上，它是 P(A|B) = [P(B|A) * P(A)] / P(B)，其中P(A|B)是在B发生的情况下A发生的条件概率。 2. 条件概率的应用: - 在朴素贝叶斯分类中，条件概率被用来确定一个样本属于特定类别的可能性。例如，对于新的输入特征向量x，朴素贝叶斯计算每个类别的概率P(c|x)，其中c是类别，x是特征向量。 3. 分类决策: - 朴素贝叶斯分类器根据每个类别的后验概率P(c|x)进行决策，选择具有最高后验概率的类别作为预测结果。如果p1(x|c1) > p2(x|c2)，则分类为c1，反之则为c2。 4. 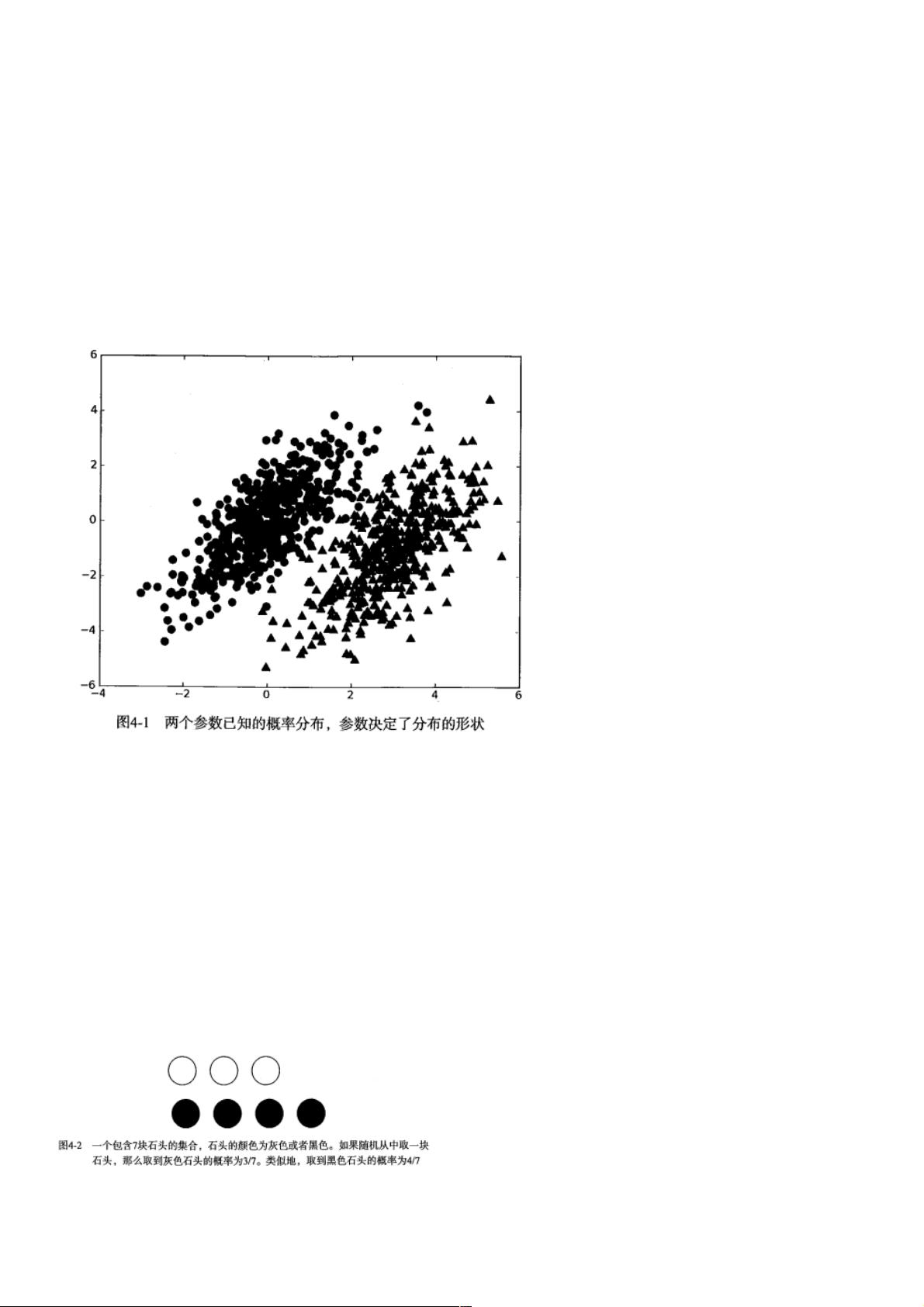条件概率的实际例子: - 如何计算在已知桶B中有石头的情况下，取到白色石头的概率（P(white|bucketB)），这是条件概率的一个应用。朴素贝叶斯算法用这个概念来调整特征之间的概率影响。 5. 算法优势: - 朴素贝叶斯算法的计算效率高，因为它只需要存储每个特征在每个类别下的概率，而无需存储所有可能的联合概率。这使得它在处理高维数据时非常有效。 6. 局限性: - 朴素贝叶斯假设特征之间相互独立，但这种独立性在现实中往往不成立，可能会导致模型性能降低。然而，通过特征选择或正则化技术，有时可以缓解这个问题。 朴素贝叶斯是一种实用的分类工具，特别是在处理大规模数据和高维特征空间时，它的高效性和简洁性使其成为首选。在Python中，可以利用scikit-learn库中的`GaussianNB`、`MultinomialNB`等函数实现朴素贝叶斯分类。理解并掌握这些概念对于在实际项目中应用朴素贝叶斯至关重要。