自定义MATLAB实现FFT算法详解及步骤

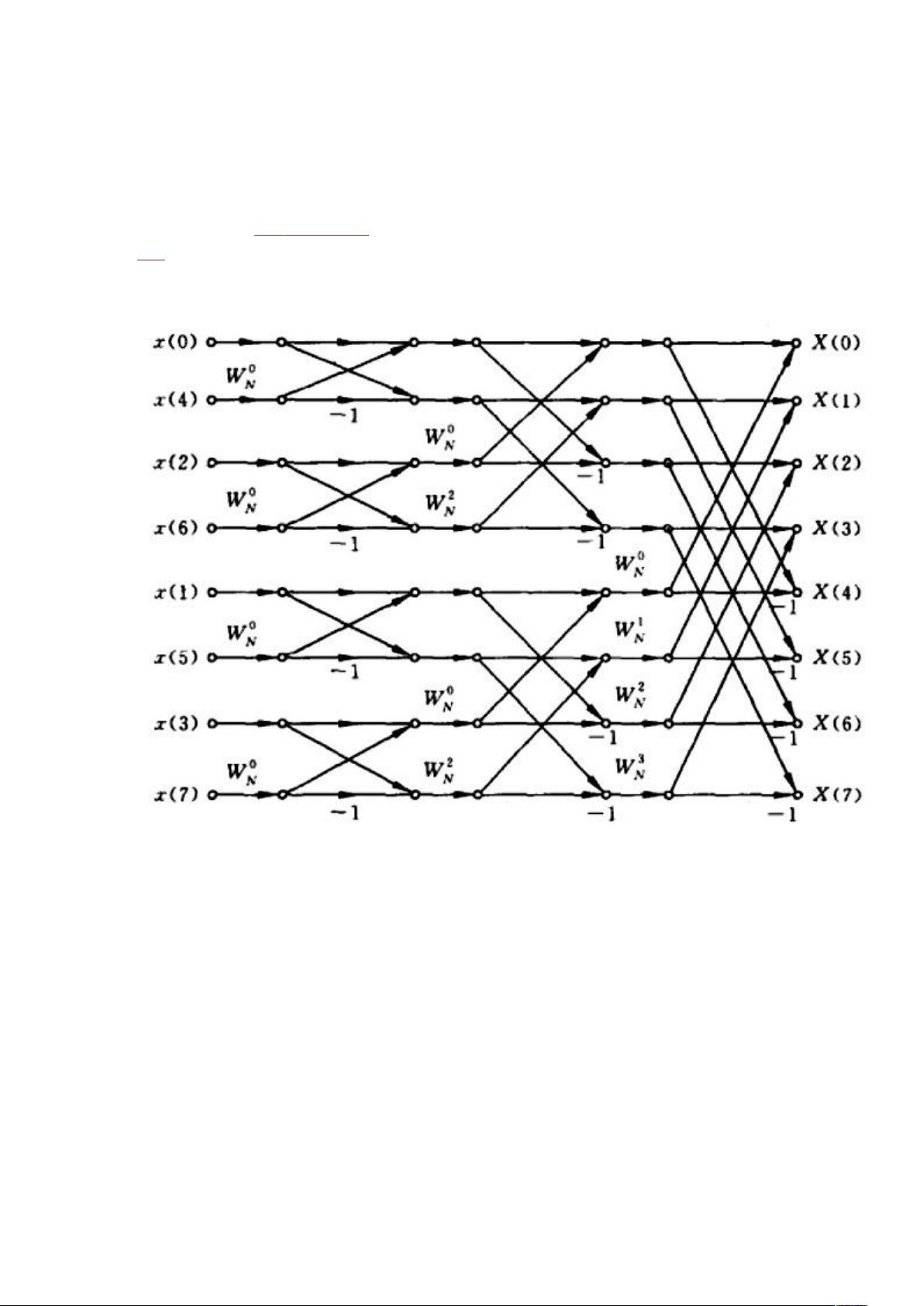
FFT (Fast Fourier Transform) 是一种高效的离散信号频域分析工具，尤其在信号处理、通信和图像处理等领域广泛应用。在这个MATLAB实现的FFT程序中，作者并未依赖MATLAB内置的fft函数，而是选择独立编写，以加深理解FFT的工作原理。 程序的核心部分首先涉及位逆转操作，这是FFT算法的预处理步骤，目的是为了优化蝴蝶（Butterfly）操作的并行性。位逆转函数接受两个参数，Nbit代表位逆转的位数，num则是待逆转的数值。通过位移和位与操作，将二进制位顺序反转，确保后续的DFT（离散傅立叶变换）计算能够按照正确的频率分量进行。 FFT算法的实现采用的是DIT (Decimation in Time) 方法，其基本思想是将大问题分解成多个小问题逐级解决。对于8点FFT为例，它分为三个层次的循环：外层循环i控制阶数（从0到log2(PointNum)-1），中间层循环j对应于每阶DFT中的组数，而内层循环k则确定每组内的蝶形运算次数。例如，8点FFT中，第一阶有1组，第二阶2组，第三阶4组，依次递增，直到最后一阶所有数据都在一组中。 在DIT-FFT过程中，旋转因子的选择至关重要，它根据输入数据的长度和蝴蝶操作的阶段来确定。对于N点DIT-FFT，旋转因子W通常取为W = ei * 2π/N，其中i从0到N/2-1。这些旋转因子用于调整信号的相位，确保变换的正确性。 蝶形运算设计是FFT的核心，依据信号流图，计算公式包括乘法和加法操作。在给出的代码片段中，我们看到一个示例算式，如X(k+1) = X(k) + W^(-j) * X(k-N/2+j)，这是计算蝴蝶操作的一部分，它涉及到输入序列X[k]的递推更新。 整个程序中，还创建了一个示例场景，用512个采样点的信号进行计算，包括了信号生成和FFT运算。通过这个过程，读者可以深入了解如何在MATLAB环境中手工实现FFT算法，以及如何利用位逆转和蝶形操作来完成频域分析。 这个MATLAB FFT实现展示了从底层原理到实际编程的全过程，对于学习和理解FFT算法的运作机制非常有价值。