东北大学自动控制原理课件：时域分析与阶跃响应

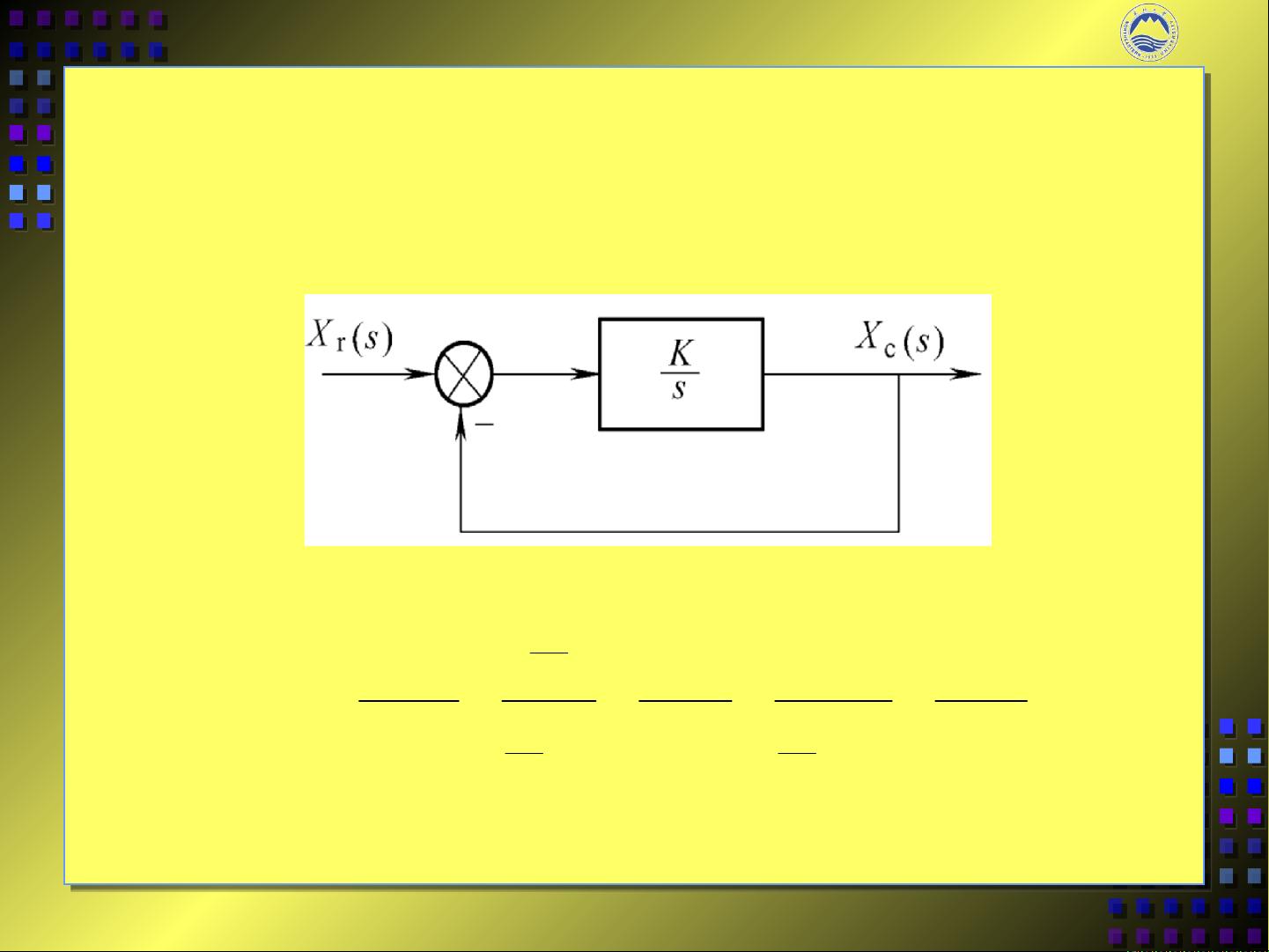
"东北大学自动控制原理课件，主要讲解第三章自动控制系统的时域分析，包括系统的稳定性、暂态特性和稳态特性，重点是一阶、二阶及高阶系统的阶跃响应，并介绍了自动控制系统的代数稳定判据和稳态误差。课件适合准备考取东北大学自动化专业的学生学习。" 自动控制系统的时域分析是控制系统理论中的关键部分，它通过对系统响应的分析来评估其性能。时域分析方法依赖于微分方程的求解，以获得系统的动态响应。这种方法简单直观，尤其适用于一阶和二阶系统，但处理高阶系统时则相对复杂。 时域分析关注的主要指标有稳定性、暂态特性和稳态特性。稳定性是控制系统的基础，确保系统在受到扰动后能够返回到稳定状态。暂态特性涉及系统从初始状态过渡到稳态的过程，包括上升时间、超调和调节时间等。稳态特性则关注系统在长期运行中的表现，特别是稳态误差，即系统在长时间运行后能否达到期望的输出。 一阶系统的阶跃响应是时域分析中的一个重要主题。这类系统的时间常数\( T \)影响着响应的速度。调节时间\( ts \)定义了系统响应达到特定稳定水平所需的时间，如5%或2%误差带。较小的时间常数意味着更快的响应速度和更好的性能。例如，在一个例子中，通过调整系统的反馈系数，可以实现特定的调节时间要求。 此外，课件中还提到了二阶系统的阶跃响应，虽然这部分内容被提到前面讲解。二阶系统在实际工程中有广泛应用，其性能指标包括超调、峰值时间和阻尼比等，这些指标对于理解和优化系统动态行为至关重要。 二阶系统的暂态响应通常包括两个重要参数：自然频率和阻尼比。自然频率决定了系统的固有振荡频率，而阻尼比影响系统的衰减程度。高阻尼系统会快速无振荡地达到稳态，而低阻尼系统可能经历显著的超调。 至于高阶系统，尽管它们的时域分析较为复杂，但通常可以通过简化或近似方法处理，使其表现得类似于一阶或二阶系统，以便进行分析。 自动控制系统的代数稳定判据是用来判断系统是否稳定的数学工具。这些判据通常基于系统的传递函数或特征根的位置，如Routh-Hurwitz判据和劳斯判据。如果所有特征根位于s平面的左半平面，那么系统是稳定的。 最后，稳态误差是衡量系统输出与期望输出之间的长期偏差。它取决于系统的开环增益和闭环极点位置，以及输入信号的类型。对于给定的稳态误差要求，设计师可以选择合适的控制器结构和参数以满足这些要求。 这个东北大学的自动控制原理课件详细介绍了自动控制系统时域分析的基本概念和应用，对于理解控制系统的动态行为和设计有效的控制器至关重要。