C++编程：中缀表达式转后缀表达式算法实现

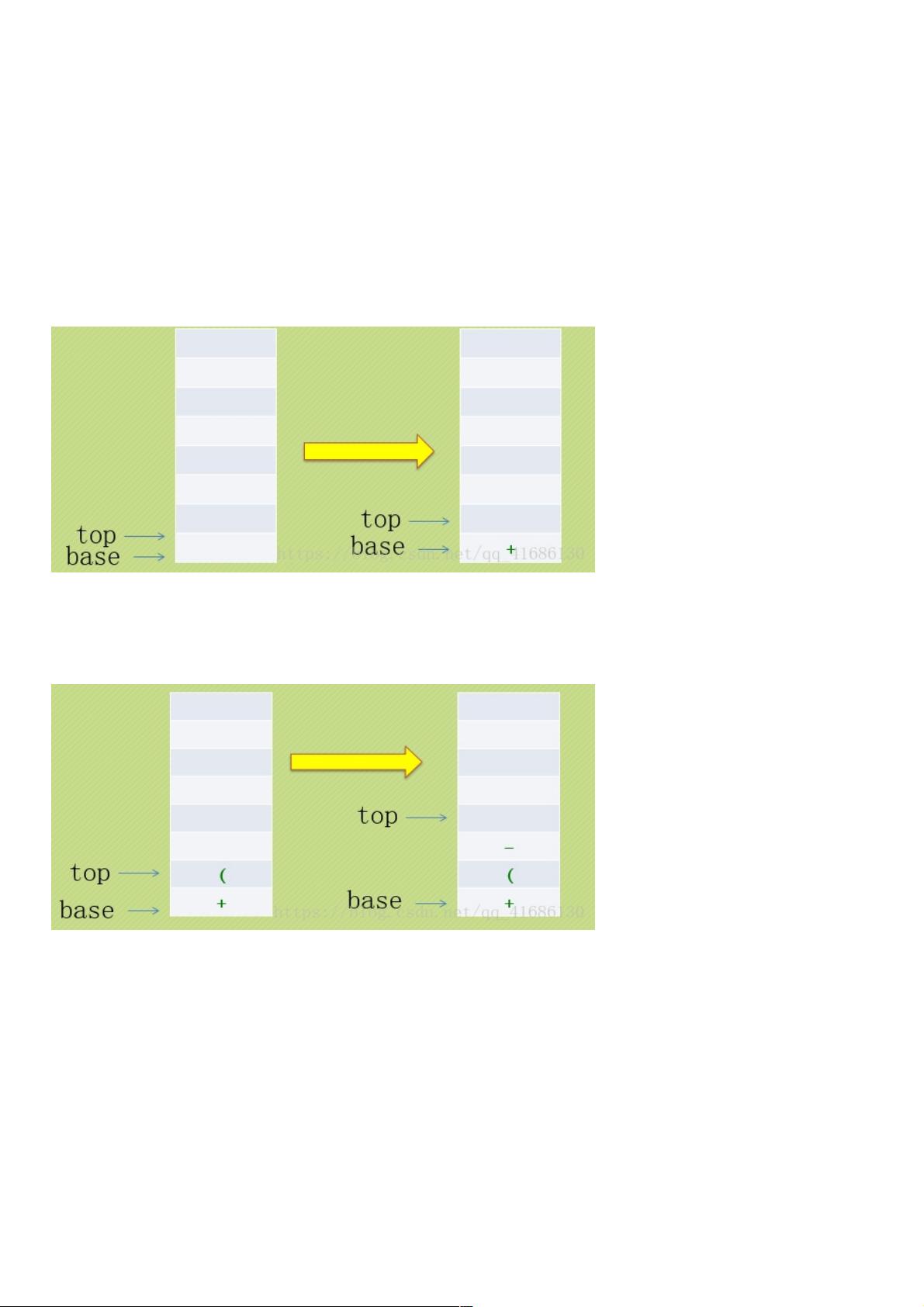
"C++利用栈实现中缀表达式转后缀表达式" 在计算机科学中，中缀表达式和后缀表达式是两种表示算术表达式的方式。中缀表达式是我们通常所熟悉的，例如 "1 + (2 - 3) * 4 + 10 / 5"，其中运算符位于操作数之间。后缀表达式，又称逆波兰表示法，将运算符放在操作数之后，例如 "1 2 3 - 4 * 10 5 / +"，这样可以避免使用括号来明确运算顺序，因为运算符的优先级和结合性已经决定了计算顺序。 要将中缀表达式转换为后缀表达式，我们可以利用栈这一数据结构。栈是一种后进先出（LIFO）的数据结构，非常适合处理具有优先级的运算符。以下是一个关键步骤的详细说明： 1. **初始化栈**：创建一个栈，用于存储运算符。 2. **遍历中缀表达式**：从左到右逐个读取表达式中的字符，可能是数字或运算符。 3. **处理数字**：遇到数字时，直接将其输出到后缀表达式中。 4. **处理运算符**：遇到运算符时，若栈为空或当前运算符优先级高于栈顶运算符，将运算符压入栈；否则，弹出栈顶运算符并输出，直到满足条件。对于左括号 "("，直接入栈；对于右括号 ")"，则连续弹出栈中运算符直至遇到左括号，不输出左括号。 5. **结束处理**：遍历结束后，栈中剩余的运算符依次弹出并输出。 在C++中，我们可以使用数组或动态分配的内存来实现栈。下面是一个简化的代码框架，展示了如何实现这个过程： ```cpp #include <iostream> #include <stack> #include <string> bool isOperator(char c) { // 定义运算符集合，包括数字、括号和运算符 } int getPriority(char c) { // 定义运算符优先级，如 '+' 和 '-' 为 1，'*' 和 '/' 为 2 } void infixToPostfix(std::string infix) { std::stack<char> opStack; std::string postfix; for (char c : infix) { if (isdigit(c)) { postfix += c; // 输出数字 } else if (isOperator(c)) { while (!opStack.empty() && getPriority(opStack.top()) >= getPriority(c)) { postfix += opStack.top(); opStack.pop(); } opStack.push(c); } else if (c == '(') { opStack.push(c); } else if (c == ')') { while (opStack.top() != '(') { postfix += opStack.top(); opStack.pop(); } opStack.pop(); // 弹出左括号 } } while (!opStack.empty()) { postfix += opStack.top(); opStack.pop(); } std::cout << "Postfix expression: " << postfix << std::endl; } int main() { std::string infix = "1+(2-3)*4+10/5"; infixToPostfix(infix); return 0; } ``` 这段代码中，`infixToPostfix`函数实现了中缀到后缀的转换，`isOperator`和`getPriority`函数用来判断字符是否为运算符以及获取运算符的优先级。在主函数`main`中，我们调用`infixToPostfix`处理给定的中缀表达式。 通过这样的算法，我们可以确保正确地转换中缀表达式，并生成遵循运算优先级的后缀表达式。这个方法对于解析和计算数学表达式非常有用，特别是在编译器设计和计算器应用中。