小波变换入门教程：从零开始理解

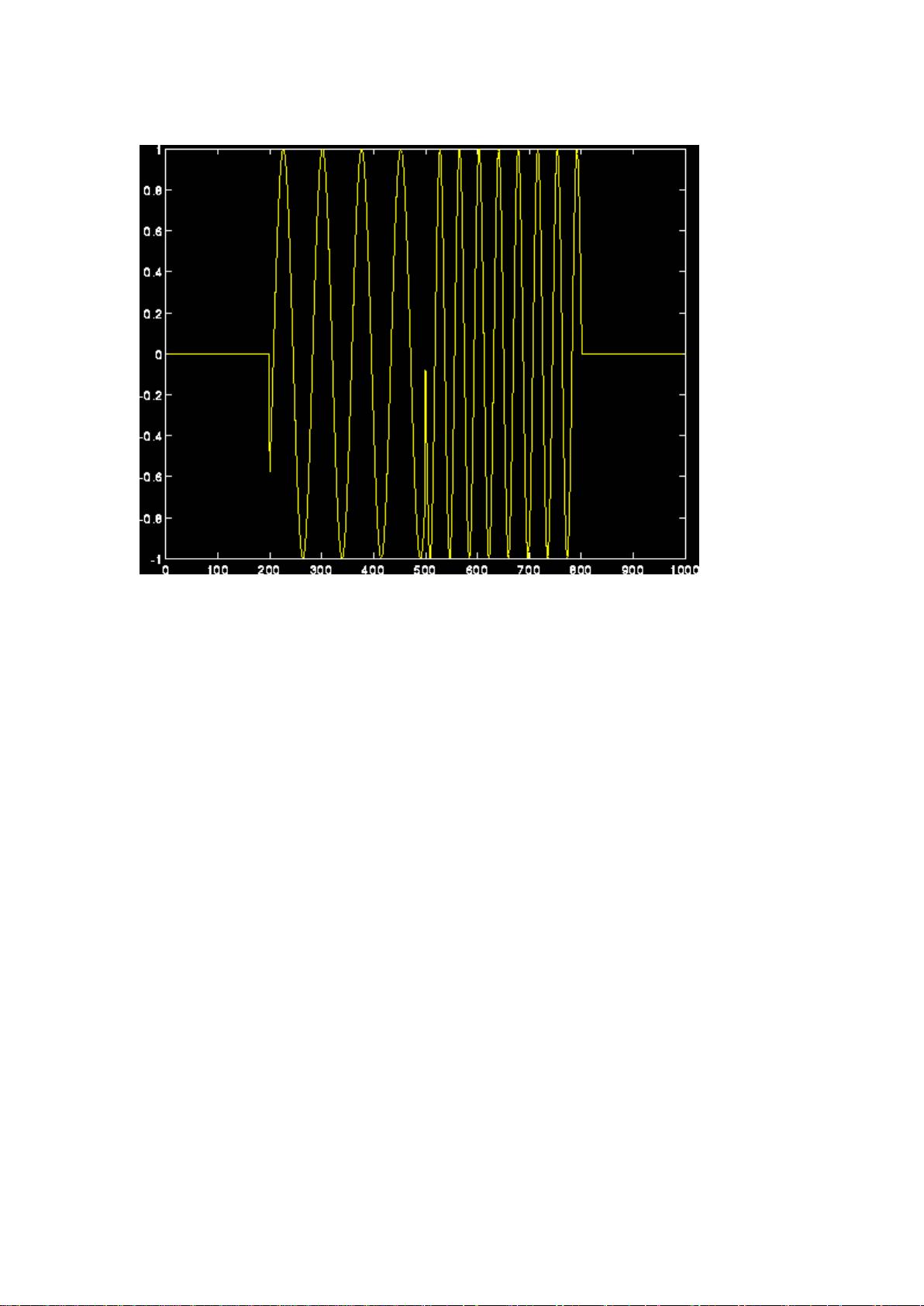
"这篇教程旨在为初学者提供一个关于小波变换的简单易懂的介绍，作者通过自己的学习经历，意识到大多数小波变换的文献难以理解，因此决定编写这个教程，帮助那些对小波变换感到困惑的人。教程的目标是阐述小波变换的基本原理，而不涉及复杂的理论证明，适合没有相关背景知识的读者。" 在小波变换的世界里，我们首先要理解“变换”的概念。变换是为了提取原始信号中不易直接获取的信息。对于信号处理，特别是时域内的信号，通过数学变换可以揭示信号的隐藏特征，比如频率信息。传统的傅立叶变换是常用的工具，它能够将时域信号转化为频域信号，显示信号的频率成分，这对于分析快速变化或含有多种频率成分的信号非常有用。 然而，傅立叶变换有一个局限，即它无法同时提供时间和频率的精细信息。这就是小波变换的用武之地。小波变换结合了时域和频域的优点，可以实现“时空”上的局部分析。与傅立叶变换不同，小波变换使用的是“小波函数”，这种函数具有有限的持续时间和宽度，能够更好地定位信号在时间-频率空间中的特性。这使得小波变换特别适用于非平稳信号（信号的统计特性随时间变化的信号）的分析，例如语音识别、图像压缩、金融数据分析等领域。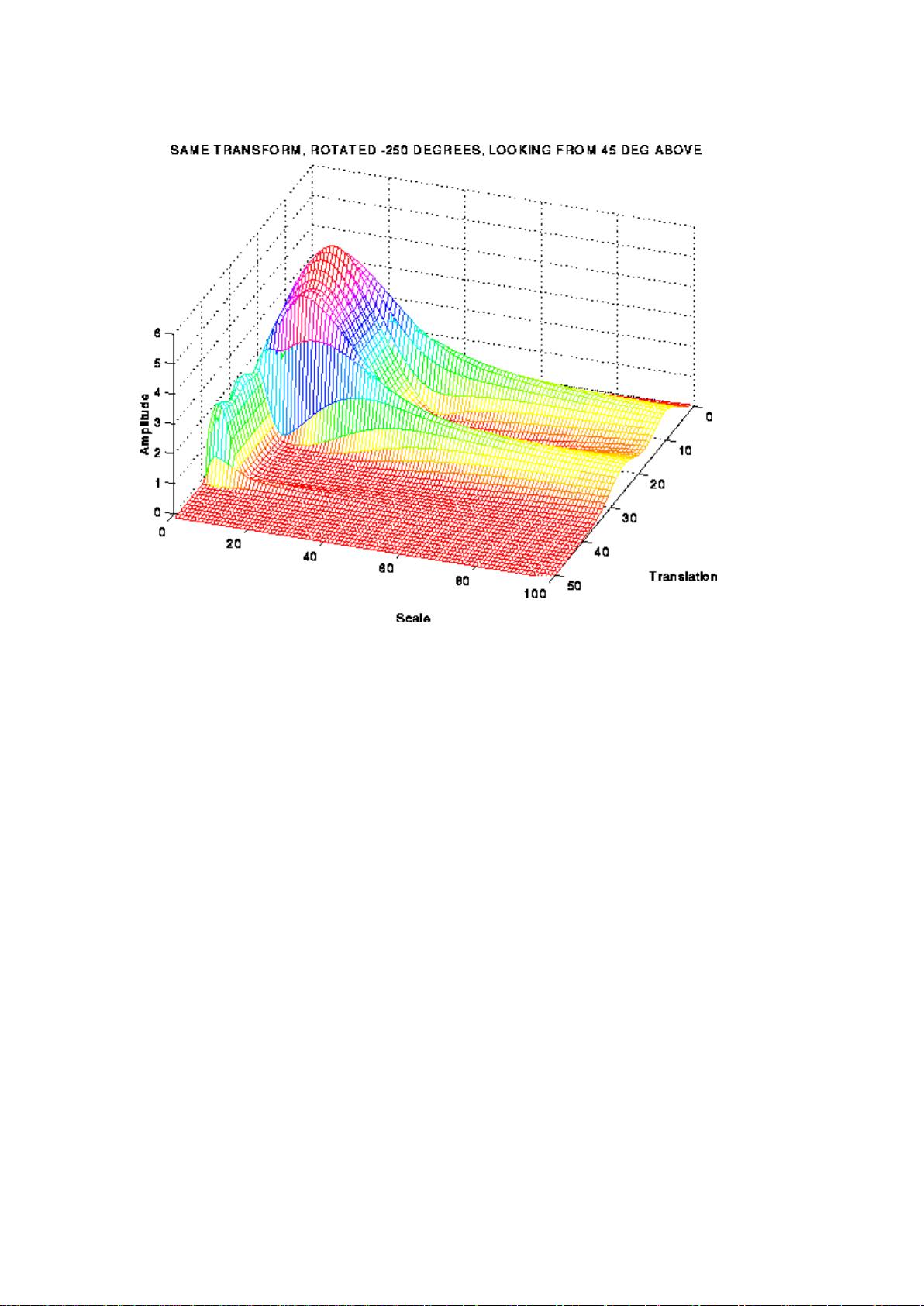 小波变换的核心在于选择合适的小波基函数，这些函数可以以不同的尺度和位置对信号进行分解。通过调整这些参数，我们可以得到信号在不同时间尺度和频率范围的详细信息。这种局部化分析的能力是小波变换相对于傅立叶变换的一大优势，它能让我们更准确地捕捉到信号在特定时刻的瞬态特征。 在本教程中，作者会逐步引导读者理解小波变换的基本思想，包括小波函数的选择、小波系数的计算以及如何利用小波变换进行信号去噪和压缩等实际应用。虽然不涉及深奥的数学证明，但会通过实例和直观的解释来帮助读者建立起对小波变换的理解。对于那些希望快速入门并掌握小波变换基本概念的人来说，这是一个很好的起点。