矩形螺纹加工实战：宏程序应用与解析

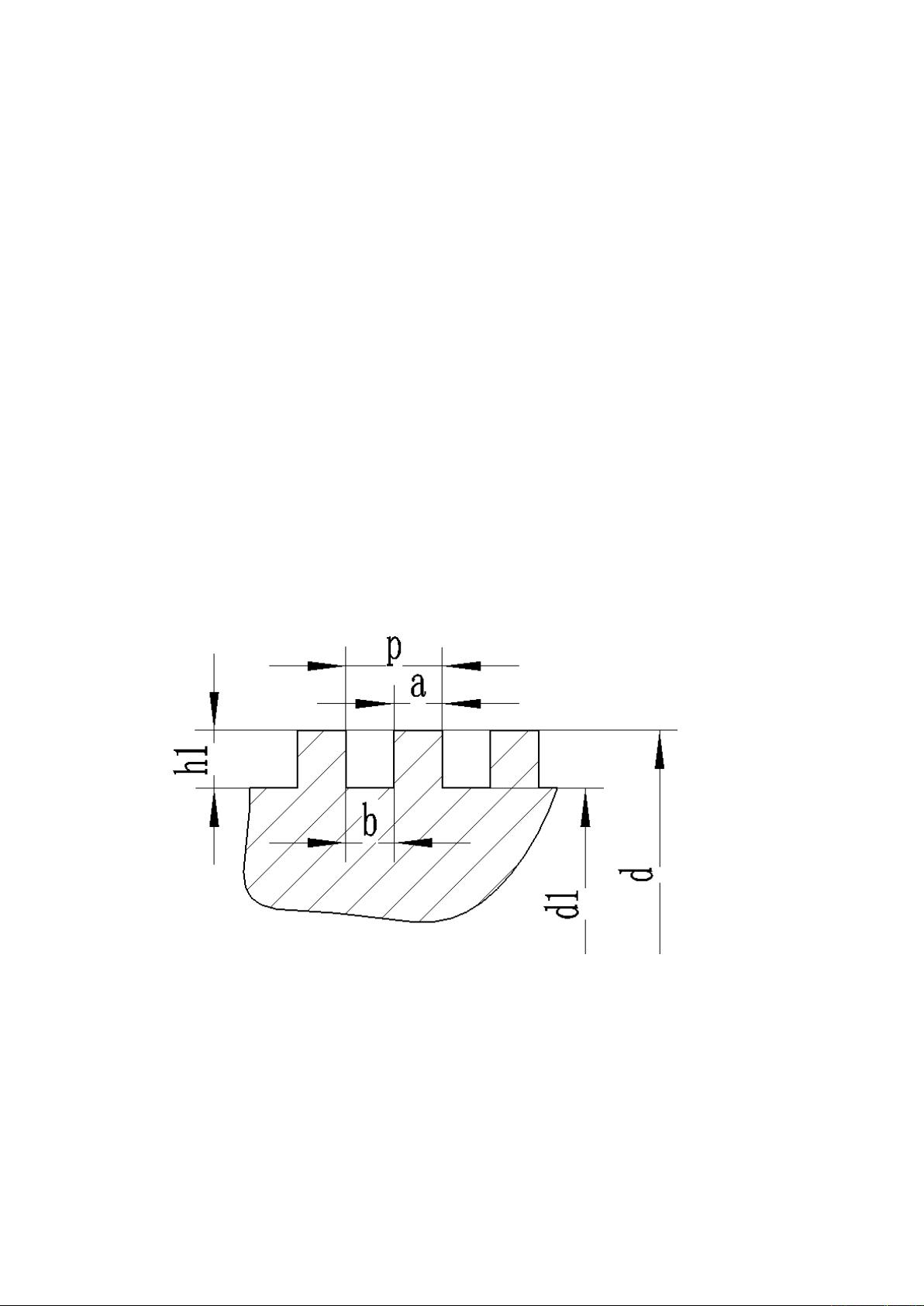
"宏程序矩形牙应用实战" 在数控加工领域，宏程序的应用极大地扩展了机床的功能，使得复杂形状的零件加工变得可能。本篇主要聚焦于宏程序在矩形螺纹加工中的实战应用，旨在帮助读者掌握矩形螺纹的参数计算、加工思路以及宏程序的编制。 矩形螺纹因其较高的传动效率而常用于传力机构，但其对中精度较低，牙根强度较弱，制造难度相对较大。尽管如此，矩形螺纹的计算相对较简单。矩形螺纹的基本尺寸计算公式如下： 1. 牙槽宽度 (b) = 0.5 * 螺距 (P) + (0.02~0.04)mm 2. 齿宽 (a) = 螺距 (P) - 牙槽宽度 (b) 3. 牙高 (h1) = 0.5 * 螺距 (P) + (0.1~0.2)mm 4. 螺纹底径 (d1) = 螺纹大径 (d) - 2 * 牙高 (h1) 以矩形50*8螺纹为例，我们可以计算出其各部分尺寸： - 牙槽宽度 = 0.5 * 8 + 0.02 = 4.02mm - 齿宽 = 8 - 4.02 = 3.98mm - 牙高 = 0.5 * 8 + 0.1 = 4.1mm - 螺纹底径 = 50 - 2 * 4.1 = 41.8mm 实际加工时，通常使用直进法，尤其是对于刀具宽度小于牙槽宽度的情况。然而，当螺距较大，牙槽宽度远超刀具宽度时，就需要采用借刀技术。借刀方法可以多样化，关键在于如何通过宏程序实现这一过程。 方法一：X向分层，Z向借刀 这种方法要求在X轴方向上分层切割，并在Z轴方向上借刀。每次切割的深度（背吃刀量）可以根据实际情况调整，例如每刀0.1mm。Z向借刀时，实际借刀长度为牙槽宽度减去刀具宽度。宏程序设计时，借刀步骤必须在X轴切深循环内完成，并确保在Z向借刀结束前X轴位置不发生变化。 在处理复杂的矩形螺纹时，宏程序编程至关重要，因为它允许精确控制刀具路径，以适应不同的工件和加工条件。例如，处理矩形60*10螺纹时，不仅需要根据公式计算参数，还需精心设计刀具轨迹和借刀策略。宏程序的编写灵活性极高，可以适应各种借刀方法，提供了极大的自由度。 通过这样的学习，不仅可以掌握矩形螺纹的计算，还能深入理解宏程序在实现特定加工任务中的作用。宏程序的应用不仅简化了复杂的编程工作，而且提高了加工精度和效率，对于提升数控加工技术具有重要意义。