掌握线性系统：输入输出传递函数详解

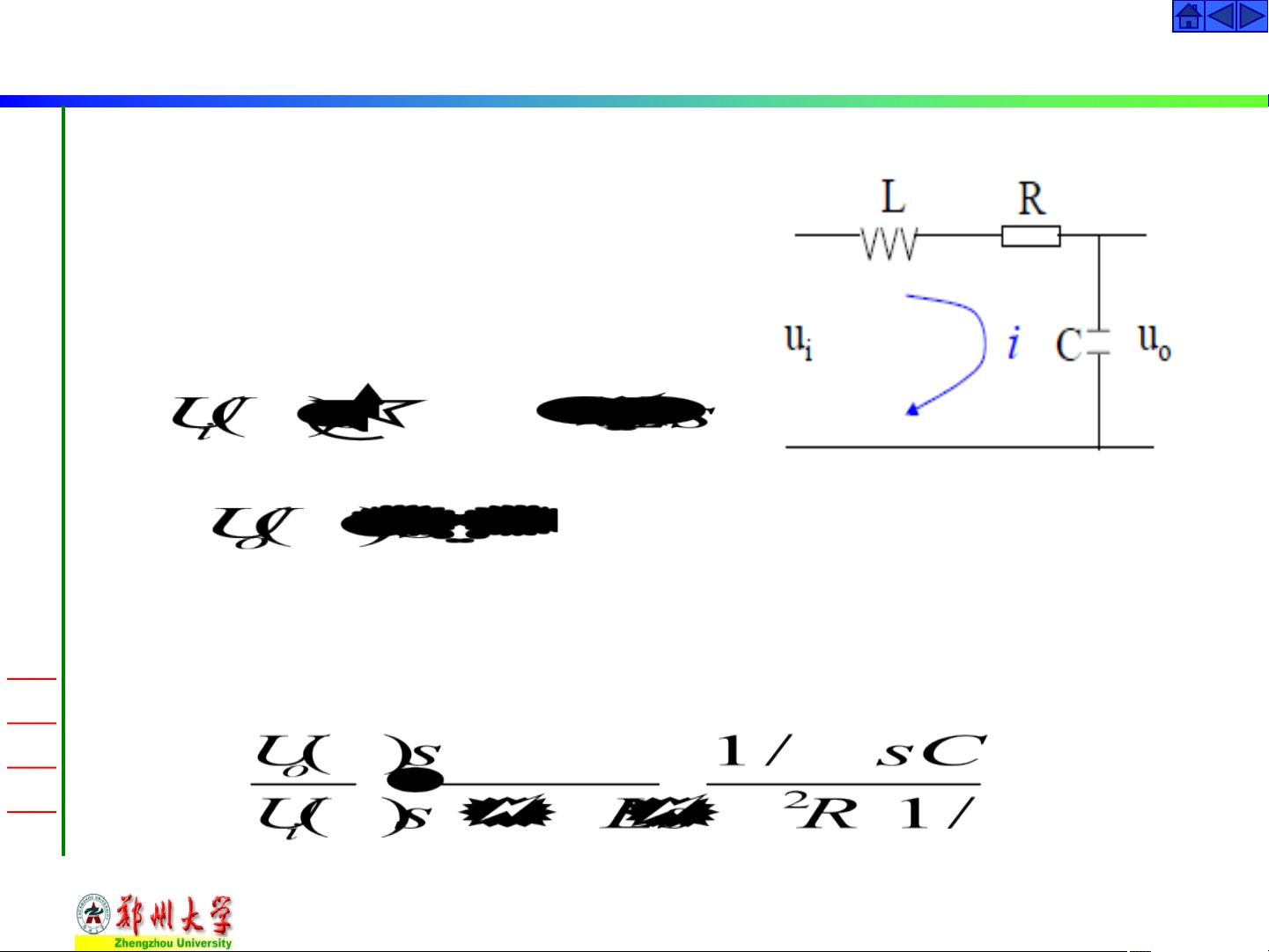
自动控制理论是电气工程学科的核心部分，本篇文档聚焦于2.2 线性系统输入输出传递函数模型。传递函数（Transfer Function）是描述线性定常系统动态特性的关键概念，它定义为系统在零初始条件下，输出信号的拉氏变换与输入信号的拉氏变换之比。通过拉氏变换，将微分方程从时域转换到复频域，使得复杂的微分关系简化为代数表达。 在一般的线性系统中，微分方程的表达式通常包含常数项和多项式的导数项，如 \( (a_0s^n + a_1s^{n-1} + \ldots + a_n)C(s) = (b_0s^m + b_1s^{m-1} + \ldots + b_m)R(s) \)，其中 \( C(s) \) 和 \( R(s) \) 分别是输出和输入的拉氏变换，\( a_i \) 和 \( b_j \) 是相应的系数。传递函数 \( G(s) \) 可以表示为 \( \frac{C(s)}{R(s)} \) 或 \( \frac{b}{a} \)，其中 \( b \) 是系统的特征多项式（分母多项式），而 \( a \) 是系统动态响应的主导部分。 传递函数的几个重要特性包括： 1. **定义来源**：传递函数是由系统微分方程在零初始条件下经拉氏变换得到的，这反映了系统的动态响应与输入之间的基本关系。 2. **求解应用**：已知传递函数和输入信号，可以计算出输出的拉氏变换，通过拉氏逆变换得到时域下的输出响应，表明传递函数是连接微分方程、输入和输出的重要桥梁。 3. **特征多项式**：传递函数的分母多项式对应着微分方程的特征多项式，它提供了系统稳定性分析的关键信息，如系统是否有根在复平面上的实部为负，决定系统是否稳定。 4. **与微分方程的关系**：虽然传递函数是基于拉氏变换，但它提供了一种简洁的分析工具，与微分方程相比，传递函数更易于处理线性系统的频率响应和稳定性问题。同时，它们互为解析，即微分方程与传递函数能够相互转换，有助于理解和设计控制系统。 总结来说，线性系统输入输出传递函数模型是理解系统动态行为的基础，通过传递函数，工程师可以快速评估系统的响应特性，这对于控制系统的设计和分析至关重要。掌握这个概念对于电气工程专业学生和从业者来说，是深入理解控制系统工作原理和技术应用的关键一步。