位图矢量化算法研究：轮廓提取与曲线拟合

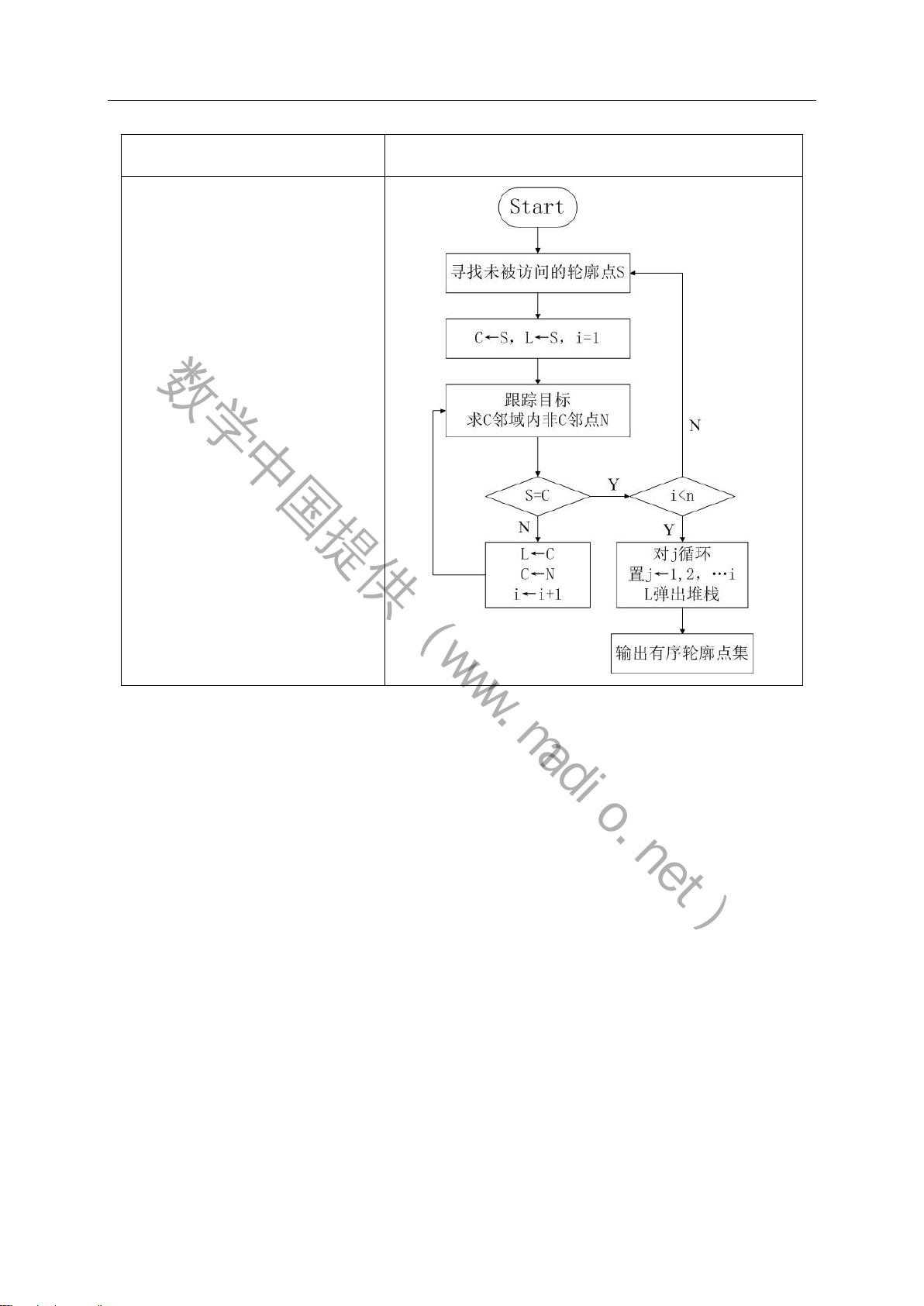
"第七届‘认证杯’数学中国数学建模网络挑战赛B题，参赛队号#1031，涉及位图文件的灰度图形矢量化问题，要求建模并表达矢量图形的边界函数方程。" 本文主要探讨的是在数学建模竞赛中的一个实际问题——位图矢量化算法的研究。位图矢量化是将像素化的图像转换为由线条、曲线和点组成的矢量图形的过程，这对于图形处理和计算机图形学领域至关重要。在本题中，所处理的图形是简单的灰度图像，这意味着图像只包含单一的灰度级别，没有颜色信息。 矢量化过程通常包括以下几个关键步骤： 1. **轮廓提取**：这是矢量化过程的第一步，目的是识别图像中的边界或轮廓。这可以通过各种边缘检测算法实现，如Canny边缘检测、Sobel算子或Prewitt算子。这些算法通过计算像素梯度或强度变化来定位图像中的突变点，从而找出可能的边缘。 2. **跟踪**：一旦找到边缘，就需要将它们连接成连续的轮廓。这可能涉及连通组件分析，确保每个轮廓都是一个完整且独立的对象。跟踪算法如Hough变换可用于识别直线或曲线，并将其连贯地追踪出来。 3. **轮廓特征**：轮廓特征提取是确定矢量图形的关键特性，如曲线的曲率、拐点和端点。这些信息对于后续的函数方程表示至关重要。特征点的检测有助于简化复杂形状，并且有利于保持图形的细节。 接下来，需要对提取的轮廓进行曲线拟合，以生成代表这些轮廓的数学函数。常见的方法包括样条插值、最小二乘拟合或贝塞尔曲线。这些函数可以精确地描述图像边界，并且在放大时仍能保持清晰，这是位图所不具备的特性。 在数学建模中，误差分析也是必不可少的。拟合后的曲线与原始图像边缘之间的差异需要被评估，以确定算法的准确性和效率。通常使用均方误差（MSE）或平均绝对误差（MAE）作为评价指标。 最后，将这些数学函数整理成易于理解和实现的形式，以便于在不同的应用中使用。这可能涉及将曲线表达式转换为参数形式或者极坐标形式，以便于计算和渲染。 总结，参赛队号#1031面临的挑战是将简单的灰度图像转换为数学上可解析的矢量图形，这个过程涵盖了图像处理、数学建模和曲线拟合等多个数学和计算机科学领域的知识。解决这个问题不仅需要扎实的理论基础，还需要对各种算法的熟练掌握以及对误差控制的理解。