数值分析第三章：范数理论与应用详解

"数值分析——第三章习题，讲解了范数理论及其应用，包括向量和矩阵范数，以及范数在工程类问题中的应用。" 在这篇内容中，我们探讨了数值分析中的一个重要概念——范数理论及其应用。范数理论在数学和工程领域有着广泛的应用，特别是在处理线性代数问题、优化算法和数值稳定性分析等方面。 首先，向量范数是用于度量向量大小的一个数学工具。在二维空间中，向量的长度可以通过欧几里得范数（2-范数）来定义，即向量各分量平方和的平方根。向量范数有三个基本性质：非负性（范数总是非负的，只有零向量的范数为零）、齐次性（标量乘以向量的范数等于标量的绝对值乘以向量的范数）和三角不等式（两个向量和的范数不大于各自范数的和）。这些性质确保了范数在数学上的合理性。 接着，介绍了几种常见的向量范数。1-范数，也称为曼哈顿距离或税收距离，是向量各分量绝对值之和。2-范数，即欧几里得范数，是向量各分量平方和的平方根，与直角坐标系中的距离概念相吻合。而无穷范数（-范数），指的是向量中最大分量的绝对值，它在处理某些问题时非常有用，比如在计算机器学习模型的权重约束时。 除了向量范数，还提到了矩阵范数。矩阵范数是将向量范数的概念扩展到矩阵上，它可以用来衡量矩阵的“大小”或“强度”。矩阵范数也有相应的性质，如保持向量范数的性质，即矩阵乘以向量的范数不会超过矩阵范数与向量范数的乘积。 在工程类问题中，范数理论的应用非常广泛。例如，在控制理论中，系统矩阵的范数可以用来分析系统的稳定性；在信号处理中，范数可以用于信号的压缩和去噪；在最优化问题中，范数作为约束条件可以确保解的质量。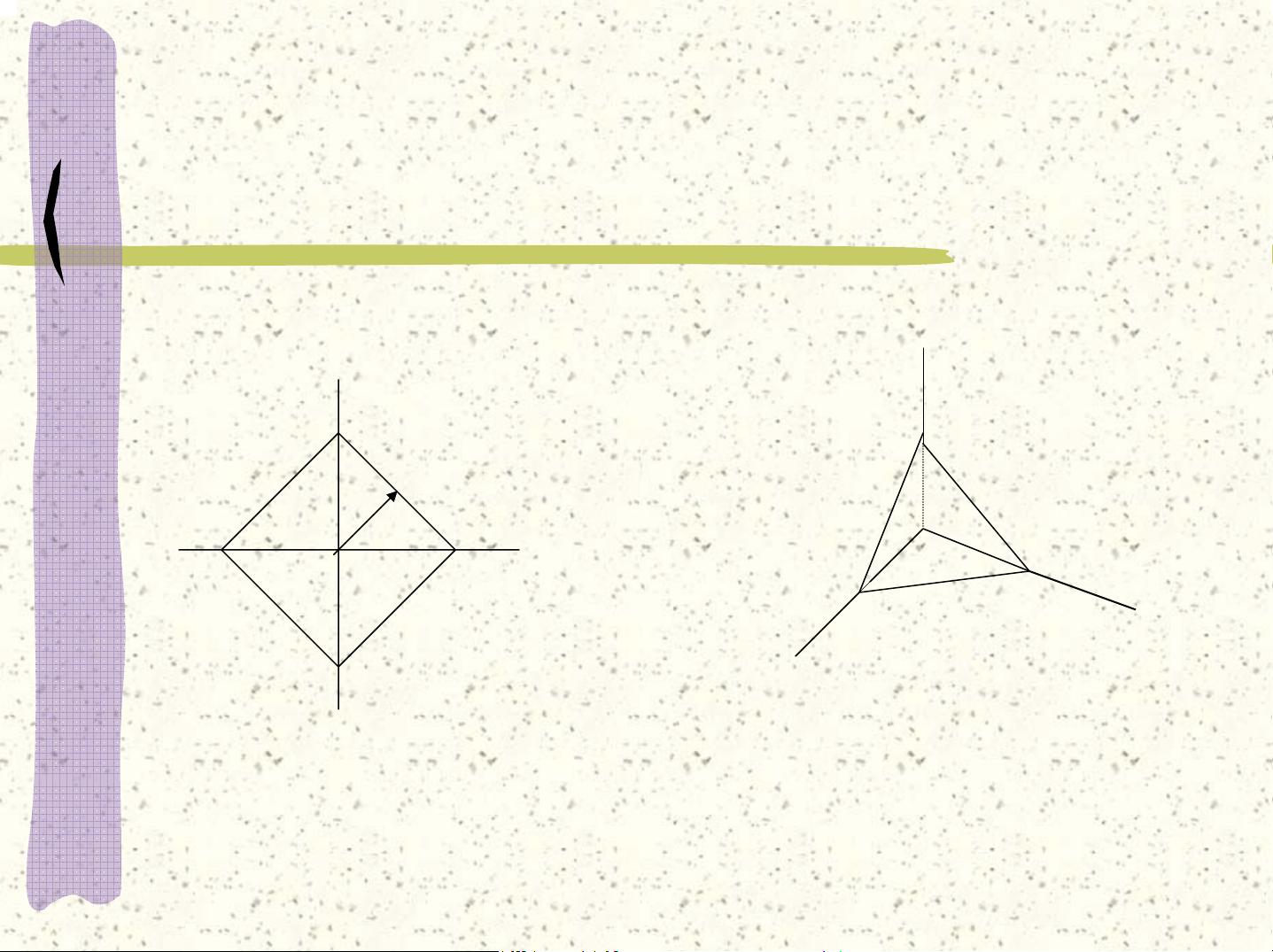 通过示例和图形（1-范数、2-范数和-范数的“单位圆”和“单位球”），我们可以更直观地理解不同范数的区别和特点。这些图形对于理解和记忆各种范数的几何含义非常有帮助。 范数理论是数值分析中的核心概念，它提供了量化向量和矩阵大小的方法，并在实际工程问题中发挥着重要作用。深入理解和掌握范数理论对于解决复杂计算问题和进行精确的数值模拟至关重要。