二叉树遍历详解：先序、中序、后序及层次遍历

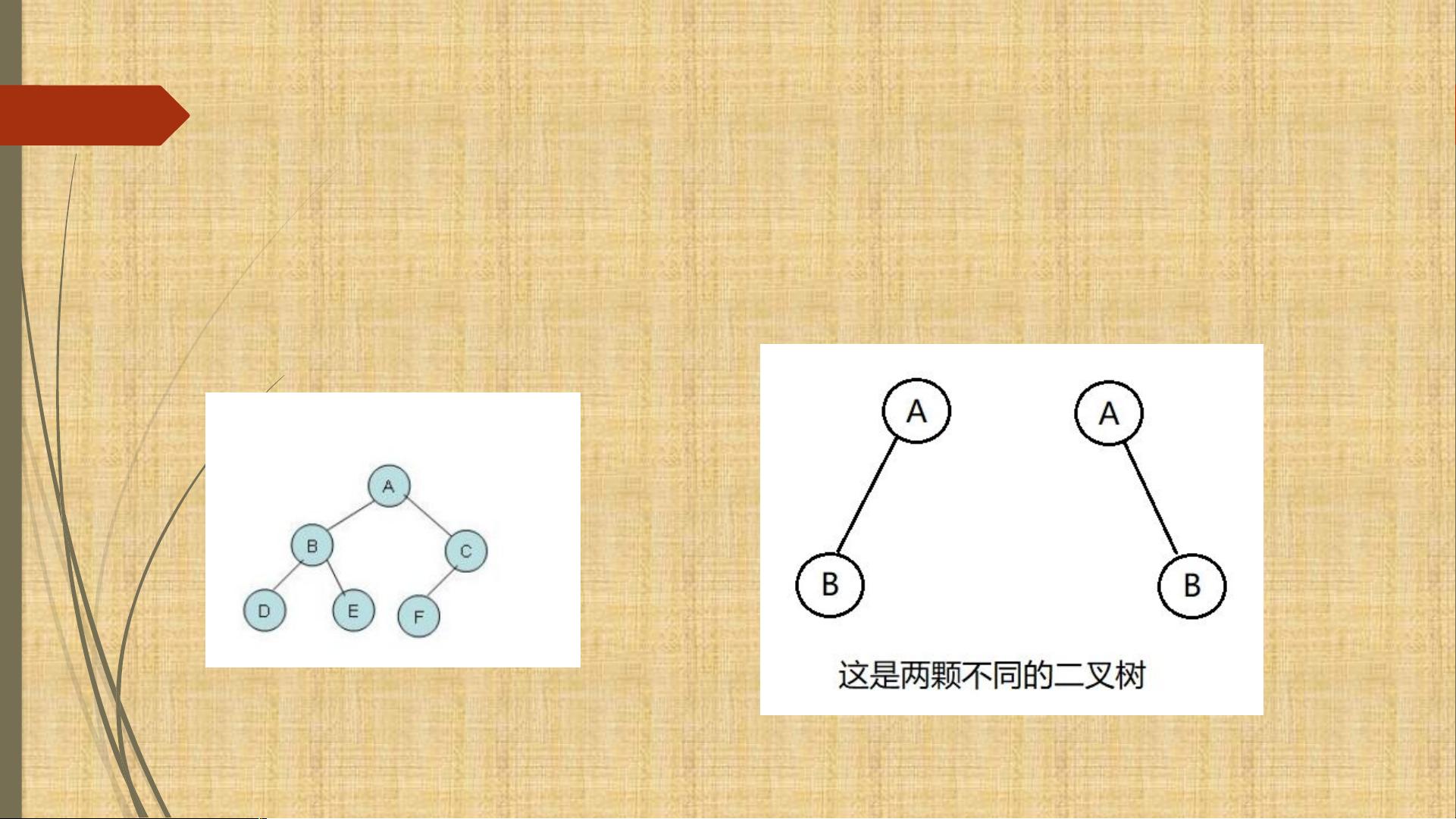
"二叉树的遍历.pptx 是一份详细介绍树和二叉树遍历的PPT，包括树的基本概念、二叉树的性质以及三种主要的遍历方法：先序遍历、中序遍历和后序遍历，并提供了Java实现代码和测试题目。" 在计算机科学中，树是一种数据结构，由n（n>=0）个有限节点组成，这些节点具有层次关系。树的特殊之处在于它没有环，每个节点最多有一个父节点，但可以有零个或多个子节点。空树是树的一种特殊情况，没有节点存在。 二叉树是树的一个特例，其中每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树有几种特殊类型，如完全二叉树，其中除了最后一层外，每一层都被完全填满，并且最后一层的所有节点都尽可能地靠左；满二叉树是所有层都完全填满的二叉树。 遍历二叉树是访问树中每个节点的过程，主要分为两种类型：深度优先遍历和广度优先遍历。深度优先遍历包括先序遍历、中序遍历和后序遍历： 1. 先序遍历（NLR）：首先访问根节点，然后递归地访问左子树，最后访问右子树。 2. 中序遍历（LNR）：首先访问左子树，然后访问根节点，最后访问右子树。 3. 后序遍历（LRN）：首先访问左子树，然后访问右子树，最后访问根节点。 广度优先遍历，也称为层次遍历，从根节点开始，按层次访问所有节点，每层从左到右依次访问。 在Java中，实现二叉树遍历可以通过递归或使用队列。以下是一个简单的Java类定义，用于构建二叉树节点： ```java public class BinaryTreeNode { private String data; private BinaryTreeNode leftChild; private BinaryTreeNode rightChild; public BinaryTreeNode(String data) { this.data = data; this.leftChild = null; this.rightChild = null; } // Getters and Setters } ``` 对于遍历的Java实现，例如先序遍历可以这样实现： ```java public void preOrder(BinaryTreeNode node) { if (node != null) { System.out.print(node.data + " "); preOrder(node.leftChild); preOrder(node.rightChild); } } ``` 同样，其他遍历方法也可以用类似的方式来实现。在实际应用中，遍历二叉树广泛用于搜索、排序、表达式求值等多种任务中。通过理解并掌握这些遍历方法，可以更好地理解和操作树形数据结构。