群体智能算法的测试函数与评估标准

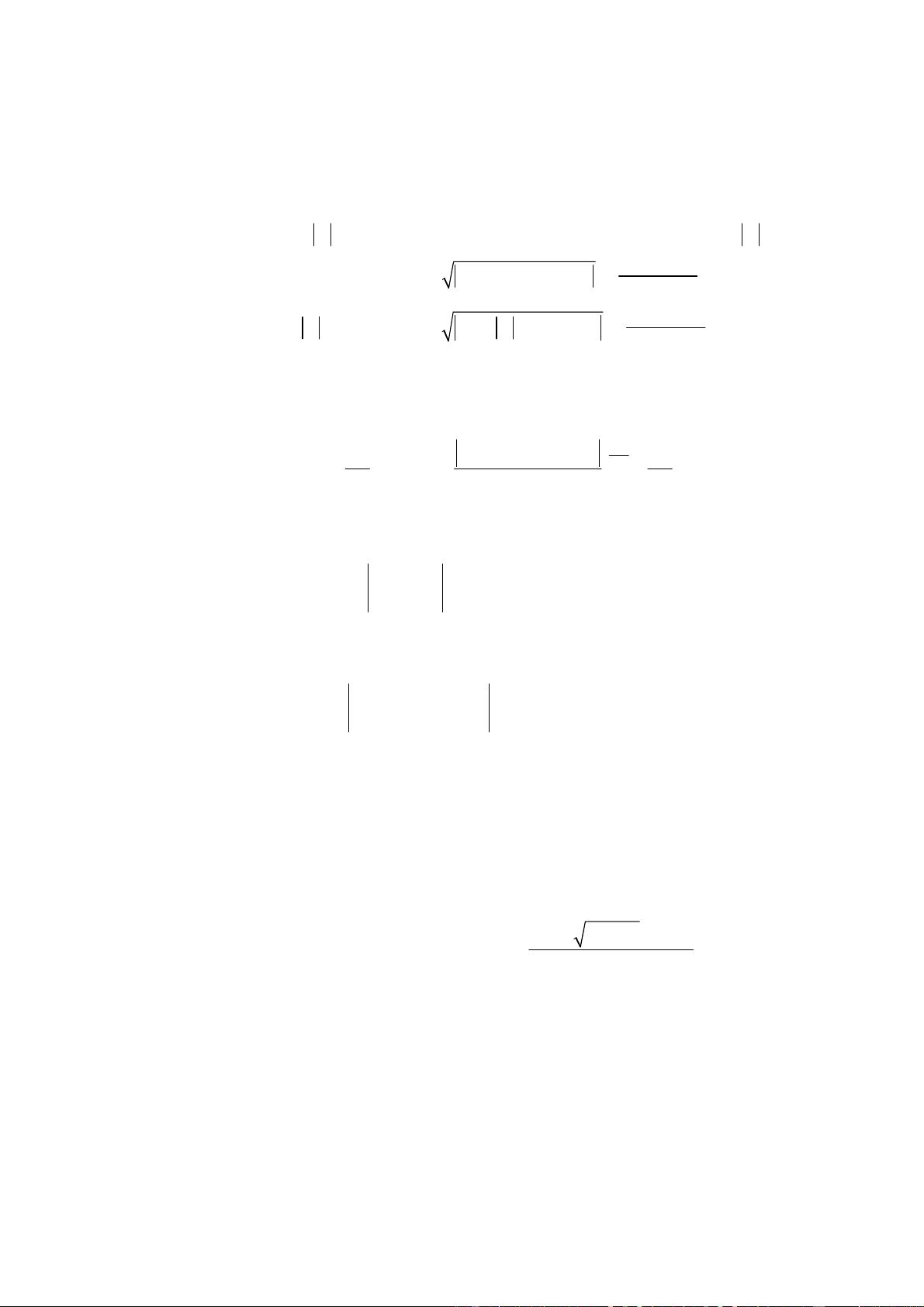
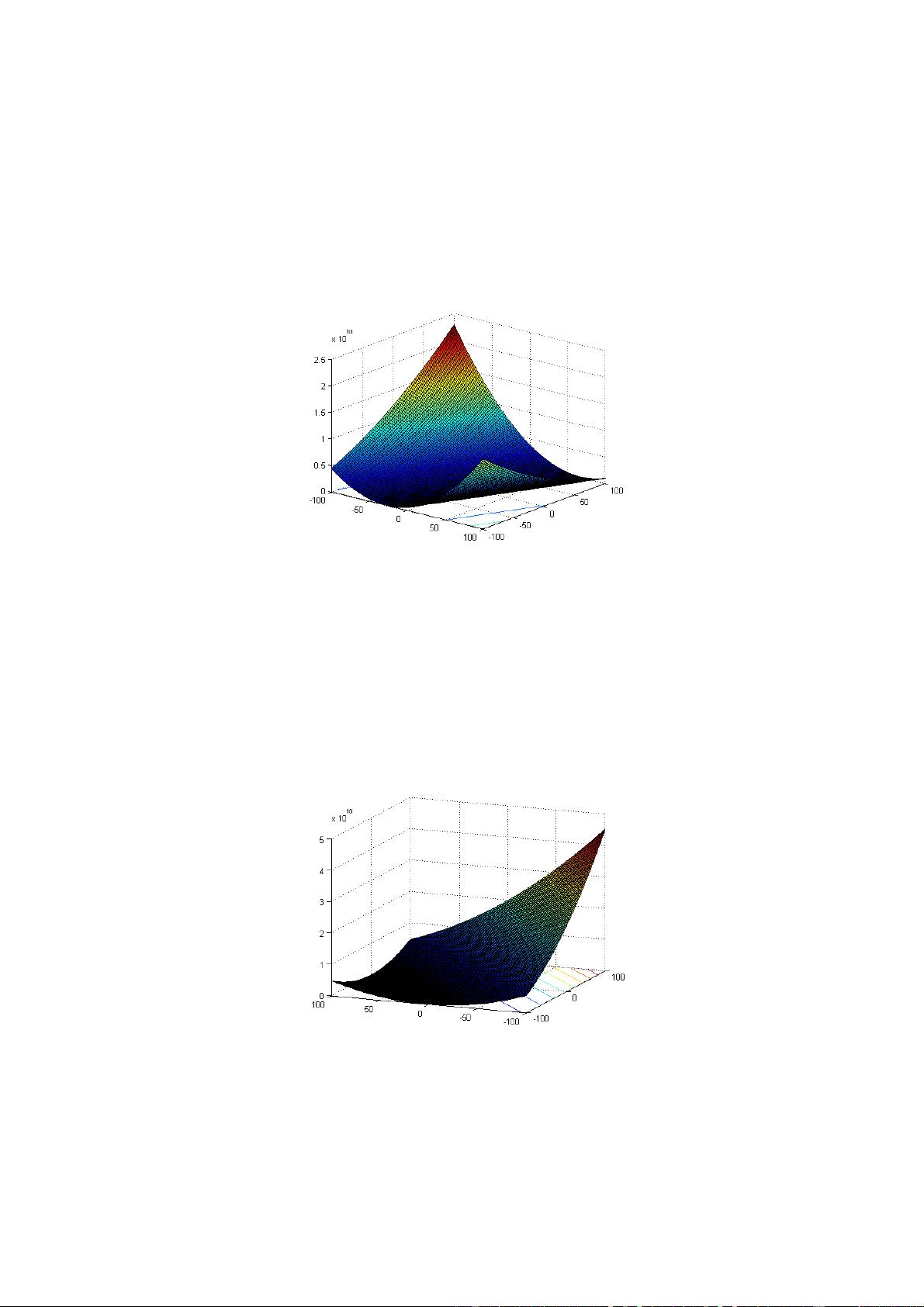
“Benchmark Functions是群体智能算法评估的重要工具，常用于单目标实参数数值优化问题。这些函数定义了问题的规范和评估标准，为不同优化算法的性能比较提供了统一的基础。” 群体智能算法，如粒子群优化（PSO）、蚁群算法（ACO）和遗传算法（GA），在解决复杂优化问题时扮演着关键角色。"Benchmark Functions"是衡量这些算法性能的标准集合，通常用于测试算法的全局搜索能力、收敛速度和稳定性。CEC 2014（国际进化计算大会）的特殊会议和竞赛专注于单目标实参数数值优化问题，这表明此类测试函数对于学术界和工业界的算法发展与比较具有重要意义。 在单目标优化问题中，算法的目标是找到一个或一组解决方案，使得特定的目标函数达到最优。测试函数的多样性是至关重要的，因为它们模拟了实际问题的各种特性，如多模态、非线性、非凸性和约束条件。例如，一些常见的基准函数包括Rosenbrock函数、Ackley函数、De Jong函数和Weierstrass函数等，每种函数都有其独特的挑战性。 Liang、Qu和Suganthan的研究报告详细描述了问题的定义和评估标准，为研究单目标优化算法提供了框架。通过这些标准，研究者可以公正地比较不同算法在处理相同问题时的表现，从而推动算法的改进和发展。此外，单目标基准问题还可转化为动态优化、分簇复合优化等问题，以进一步扩展算法的应用范围和研究深度。 在评估群体智能算法时，通常会关注以下几个关键指标： 1. 全局搜索能力：算法是否能有效地探索整个解决方案空间，找到全局最优解。 2. 局部搜索能力：算法在找到潜在最优解后，能否进行有效的微调。 3. 平均性能：在多次运行后，算法的平均结果。 4. 稳定性：算法结果的波动性，理想情况下，算法应有稳定的收敛行为。 5. 计算效率：在达到预定精度的情况下，算法所需的计算时间和资源。 这些基准函数不仅促进了优化算法的理论研究，也对工程应用中的实际问题解决提供了指导。通过不断挑战和改进现有的群体智能算法，研究人员能够开发出更高效、适应性更强的优化工具，应用于机器学习、数据挖掘、工程设计等多个领域。