数据结构习题详解：二叉树特性和哈夫曼编码

本资源是一份关于数据结构的练习题答案文档，主要包括完全二叉树的性质、二叉树的度、高度、结点数量和编号规则、线索链表的结构、森林的遍历以及二叉树的存储表示等知识点。以下是对这些内容的详细解析： 1. **完全二叉树的结点编号规则**：在完全二叉树中，若节点i为偶数且小于n，结点i的右兄弟编号为i+1；否则，结点i没有右兄弟。这一规则说明了二叉树的层次结构和节点之间的关系。 2. **二叉树的度与高度**：二叉树的叶节点数（例如4, 6, 7, 2, 5, 67）可以用来推断度为2的节点数量，但具体数值未给出。一颗二叉树有13个节点时，最大高度是完全满二叉树情况下的13（每个节点都有两个子节点），最小高度是高度为4的单支树（只有一个非叶子节点）。深度为k的二叉树最多有2^k-1个节点，深度为4的树最多15个。 3. **二叉树的深度与节点数**：完全二叉树的深度计算公式是深度= log2(n) 向上取整加1，说明如何根据节点数来确定树的深度。在二叉树中，第i层的最大节点数为2^(i-1)。 4. **线索链表与森林遍历**：线索链表是一种数据结构，用于表示二叉树的节点，通过ltag和rtag字段指示左右孩子或前后继。森林的遍历规则指出，先序遍历相当于先根遍历树的集合，而中序遍历则相当于后根遍历。 5. **二叉树的存储表示**：用二叉链表存储时，指针总数是2n个，其中n-1个用于指向孩子，n+1个为空闲指针。这表明了二叉链表的结构和空间利用。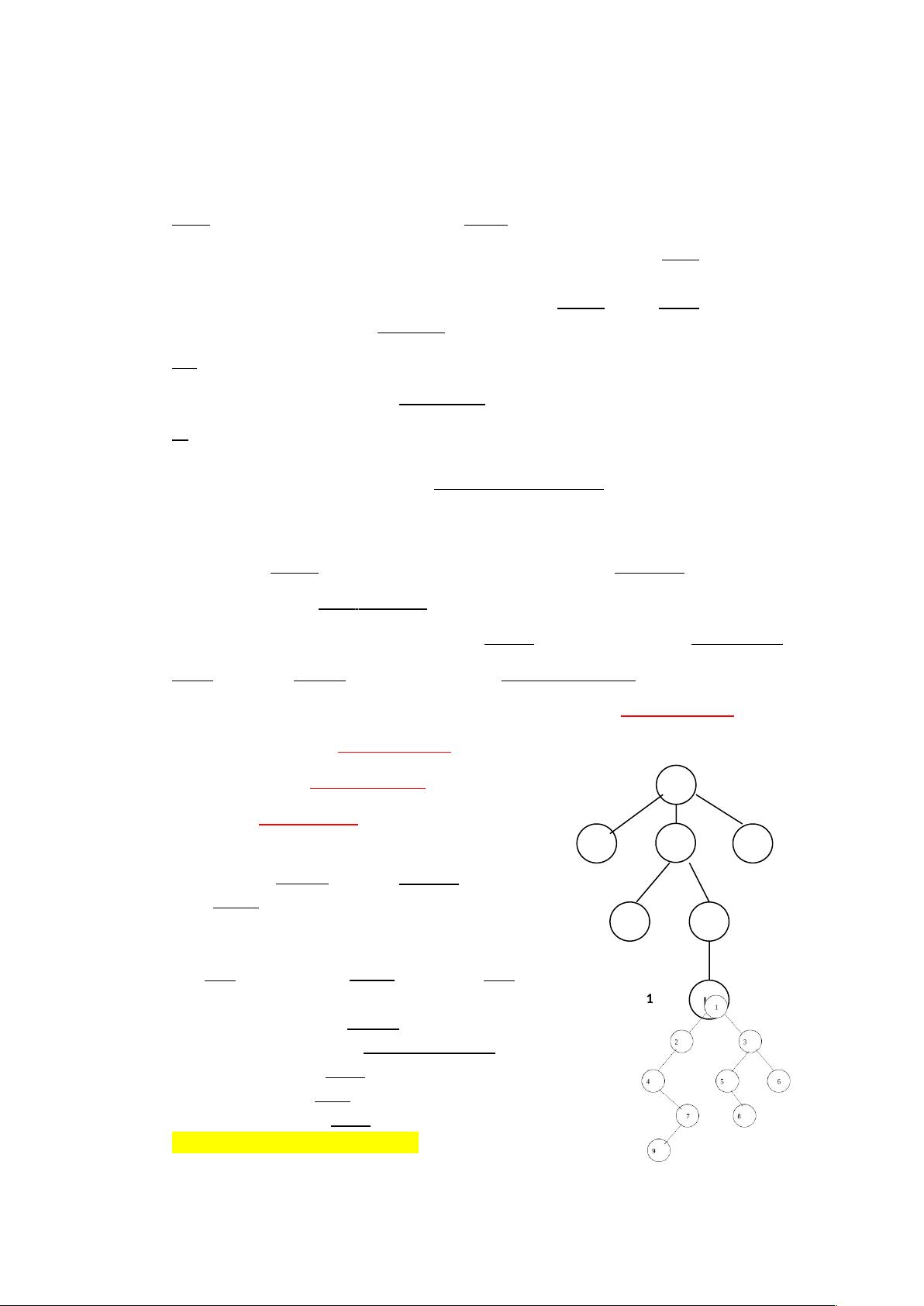 6. **树的结构分析**：题目给出了一个具体树的例子，描述了根节点、叶子节点、节点度数、树的度、深度以及广义表表示。对于二叉树的形态，需要根据中序遍历和前序遍历的序列重建树形。 7. **哈夫曼树与编码**：针对字母出现频率，需要构建哈夫曼树以实现最优的编码。哈夫曼树是带权路径长度最短的二叉树，求得的带权路径长度为261，这是设计编码的一个重要指标。 8. **树的可视化**：最后两部分涉及二叉树的可视化，一是顺序存储表示的示意图，需要将树的节点和边以线性方式展示出来；二是二叉链表存储表示，涉及到节点间的链接关系。 这份文档包含了丰富的数据结构知识，包括二叉树的基本概念、特定操作的算法以及特定数据结构的运用实例，适合用于学习和巩固这些知识点。