探索四元数：三维旋转的直观解析与MATLAB示例

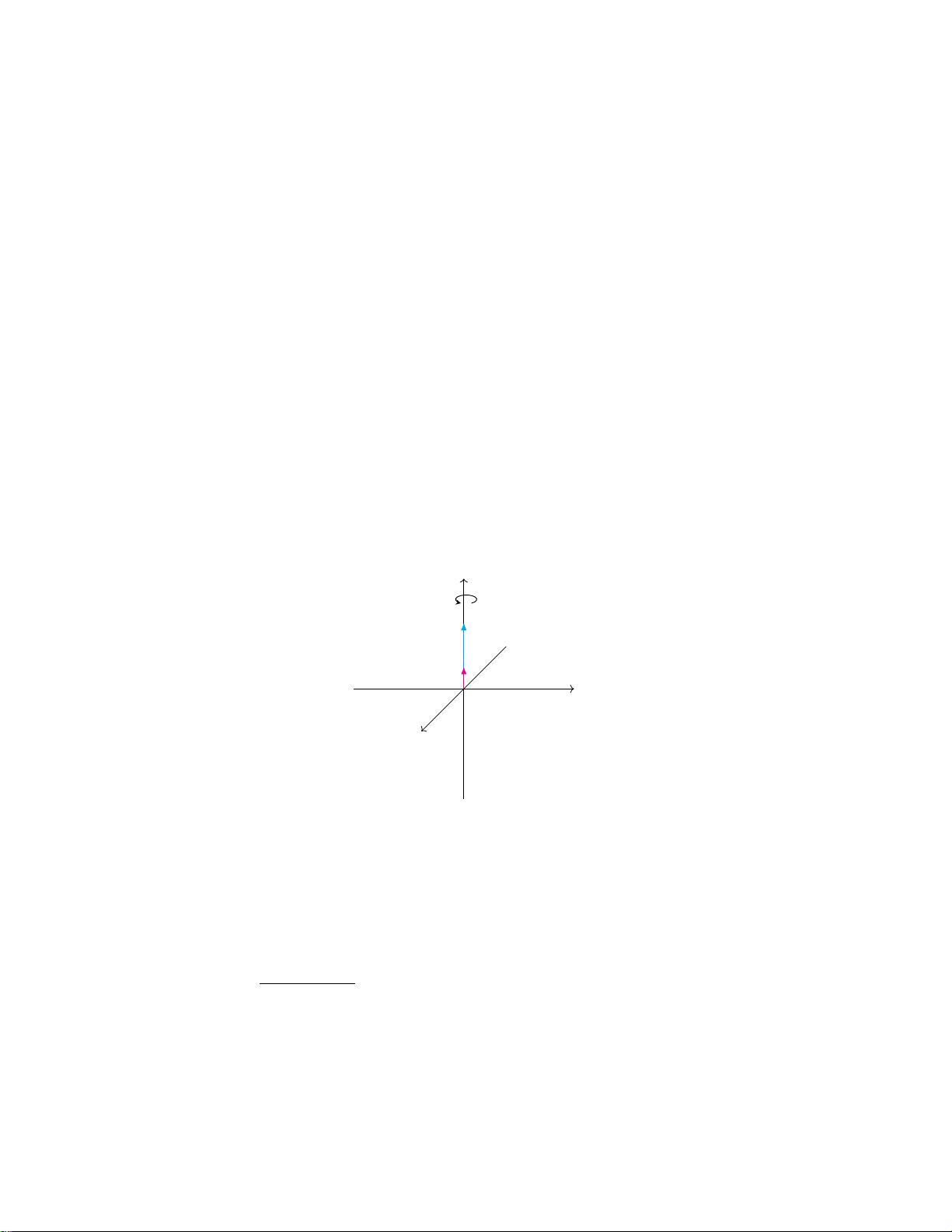
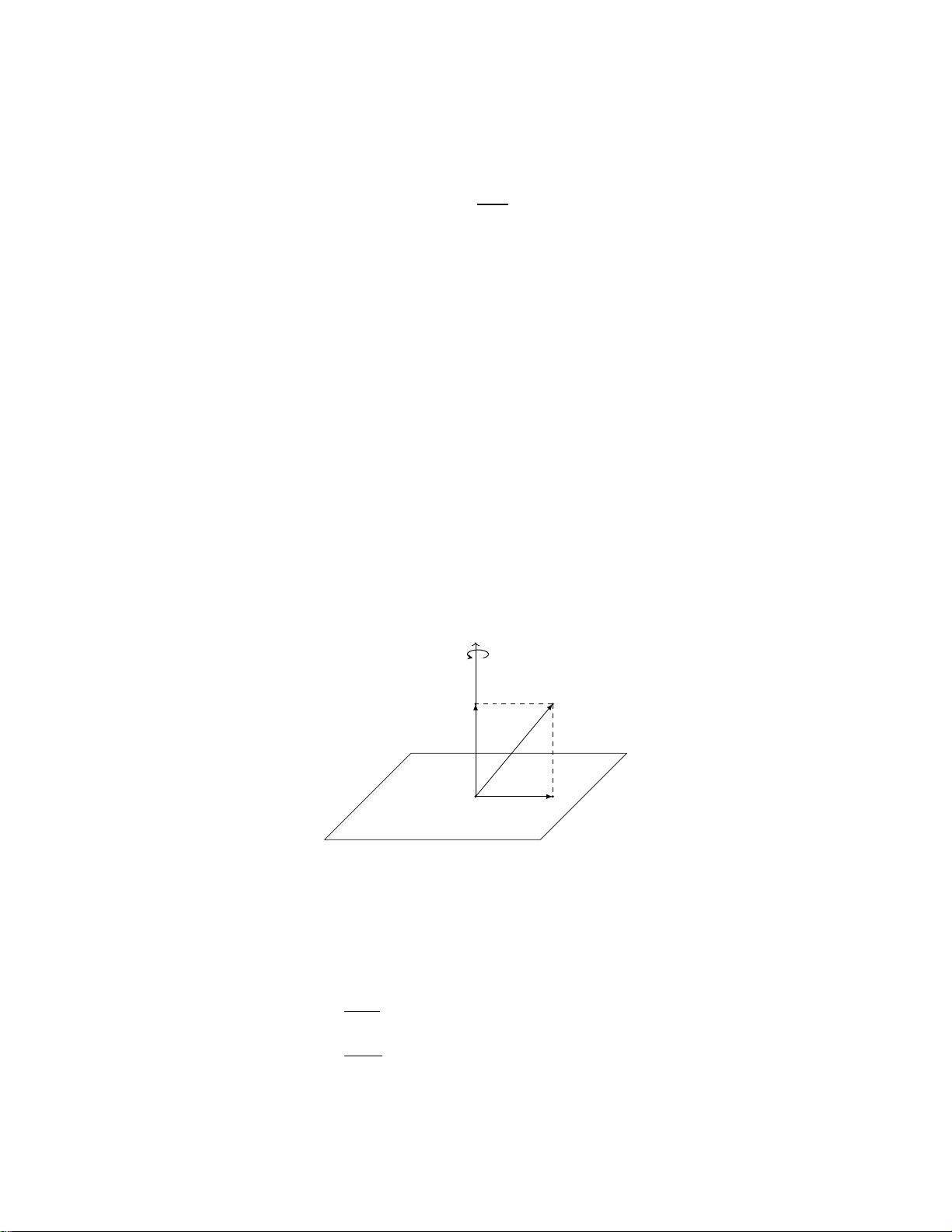
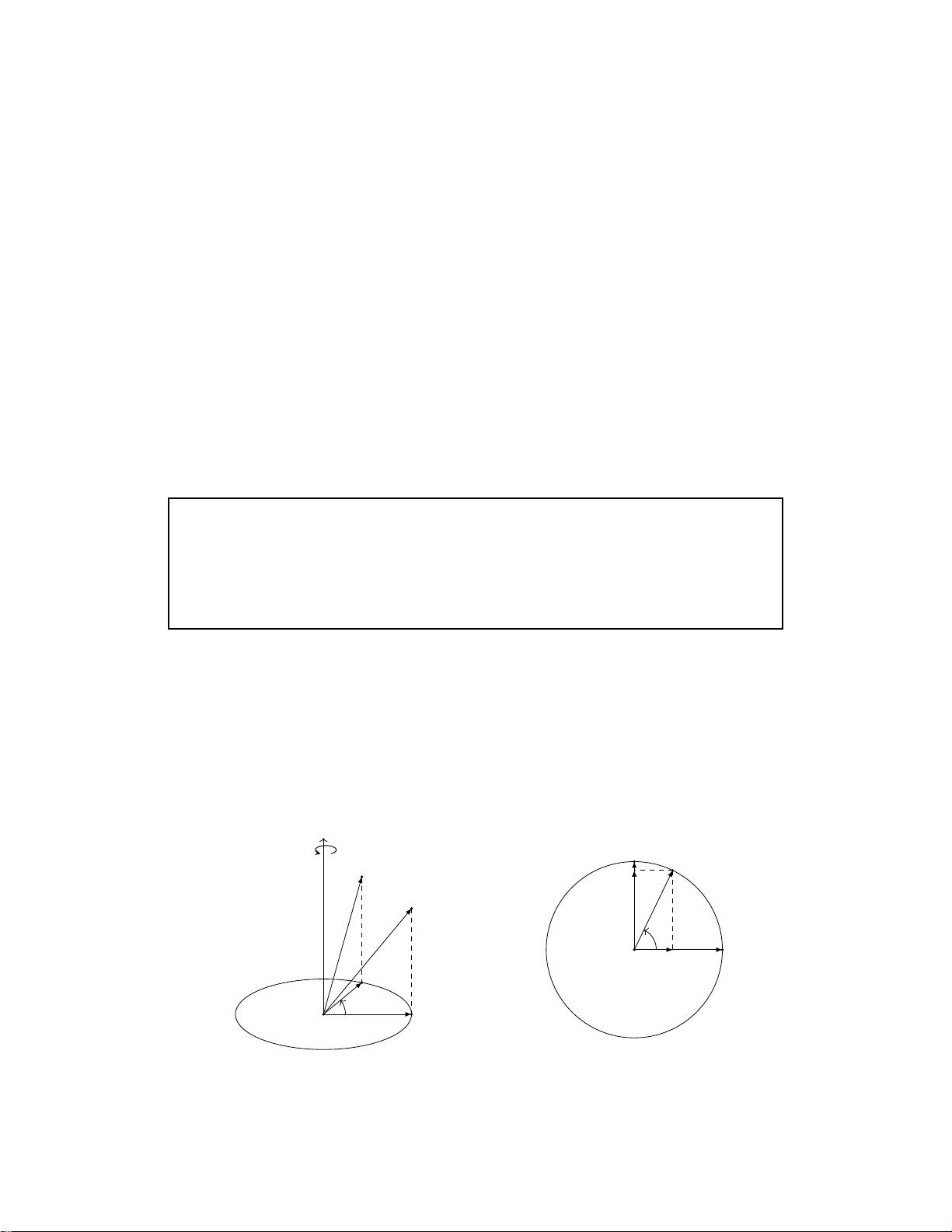
四元数（Quaternion）是一种扩展的复数系统，主要用于处理三维空间中的旋转问题。相比于传统的复数，它提供了更为高效和直观的方式来表达旋转，尤其是在计算机图形学、游戏开发和机器人技术等领域。本文将首先回顾复数的基本概念和其与二维旋转的关系，因为四元数的很多特性与复数类似。 复数由实数部分（实部a）和虚部（虚部b）组成，形式为z = a + bi，其中i满足i² = -1。复数可以视为两个实数的线性组合，也可以用向量表示为(𝑎,𝑏)T。通过理解复数的这种表示，我们可以更好地理解四元数的构造。 在进入四元数与三维旋转的关系之前，作者强调了文章会侧重于几何和实际应用，而非抽象代数理论。在三维空间中，传统的角度-轴旋转（Euler angles）可能会导致旋转顺序问题，而四元数则避免了这些问题，提供了一种连续且无奇点的旋转表示。四元数通常表示为q = w + xi + yj + zk，其中w为实部，其余三个分量(x, y, z)称为纯虚部，它们与三维空间的x, y, z轴对应。 四元数的乘法和除法遵循特定规则，使得它们可以方便地进行旋转的加法和复合。例如，两个四元数的乘积q1q2可以表示为一个旋转的组合，其中q1代表第一个旋转，q2代表第二个旋转。这在计算图形中的相机移动或物体旋转时尤其有用。 在MATLAB/Octave的示例代码中，作者展示了如何使用四元数进行旋转操作，并通过动画直观展示四元数的旋转效果。这些代码对于理解和应用四元数至关重要。尽管作者承认可能存在错误，并鼓励读者提出反馈，但他也明确了文章的版权要求，希望读者在共享和使用时遵循CCBY-NC-SA4.0协议。 本文通过对复数的简要回顾，深入探讨了四元数与三维旋转的内在联系，重点在于其实用性和在计算机图形学中的应用。通过实例和代码，读者可以更好地掌握四元数在处理三维空间旋转问题中的优势和操作方法。