设计与分析巴特沃斯低通滤波器：第6章高西全丁美玉教材解答

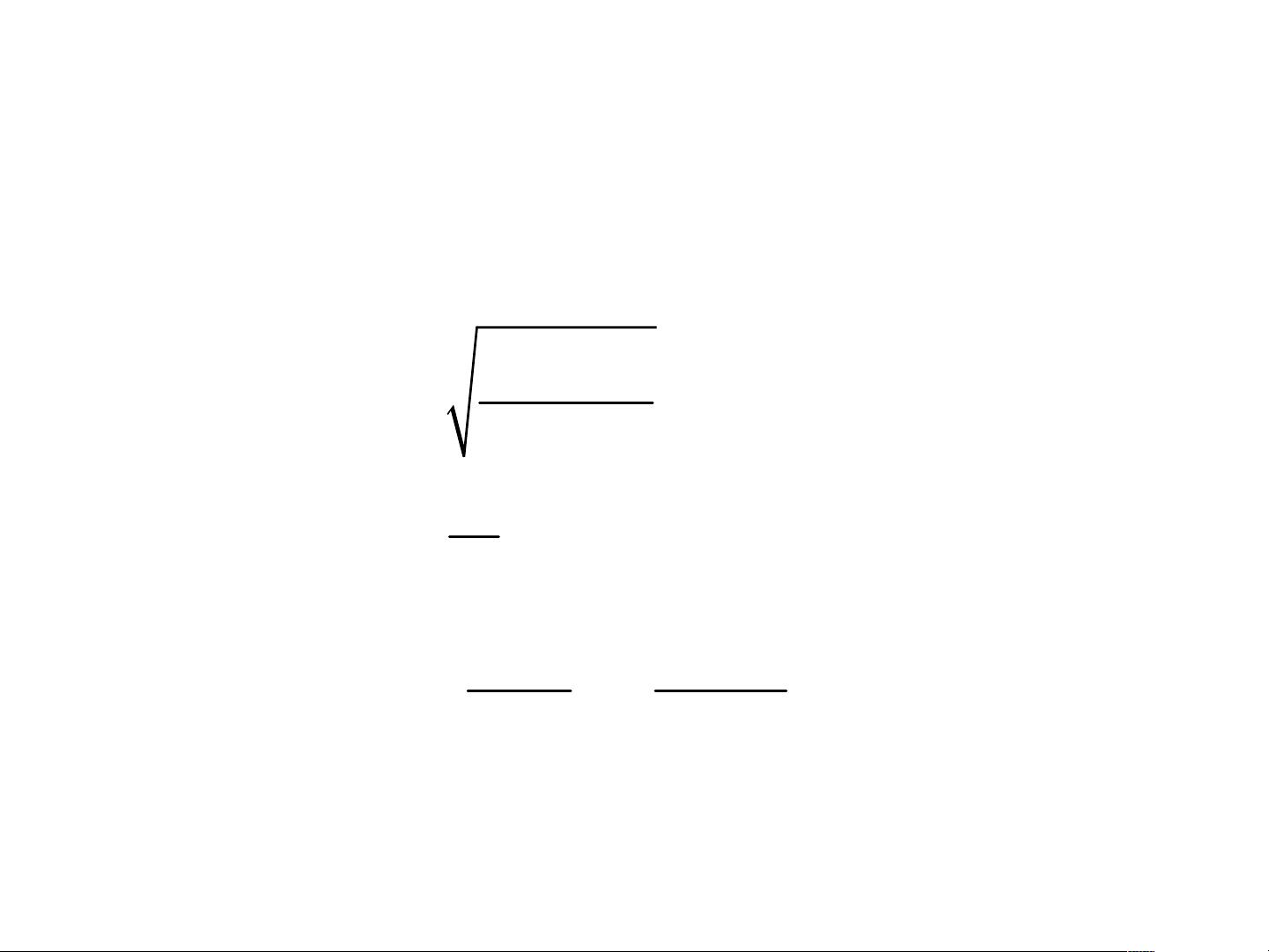
"数字信号处理课后答案 第6章(高西全丁美玉第三版)" 在数字信号处理领域，滤波器设计是至关重要的部分，主要用于去除噪声、平滑信号或者提取特定频率成分。本节内容主要涉及的是巴特沃斯低通滤波器的设计，该滤波器在通信、音频处理、图像处理等多个领域都有广泛应用。具体来说，题目要求设计一个具有特定性能指标的滤波器，包括通带截止频率、通带最大衰减以及阻带最小衰减。 1. **巴特沃斯滤波器设计**：巴特沃斯滤波器以其平坦的通带和陡峭的滚降特性而著名，是滤波器设计中常见的一种。题目中提到的滤波器要求通带截止频率`fp`为6kHz，通带最大衰减`αp`为3dB，阻带截止频率`fs`为12kHz，阻带最小衰减`αs`为25dB。设计的第一步是确定滤波器的阶数`N`，这通常通过满足指定衰减和截止频率的条件来计算。 2. **计算阶数N**：根据巴特沃斯滤波器的特性，可以使用以下公式来计算阶数： \( N = \frac{1}{2} \left[ \log_{10} \left( \frac{\alpha_s}{\alpha_p} \right) \right] \) 在此案例中，将给定的衰减值代入，得到大约4.15。通常，阶数应取整数，因此取`N=5`。然而，实际应用中可能为了简化实现电路而选择`N=4`，尽管这样会略微降低滤波器性能。 3. **归一化系统函数G(p)**：归一化系统函数是滤波器设计的关键，它将滤波器特性从物理频率转换到归一化频率。对于五阶巴特沃斯低通滤波器，可以查表得到其归一化系统函数`G(p)`，或者根据极点位置直接计算。极点位置由巴特沃斯滤波器的一般形式给出，即： \( p_k = -e^{\pm j \frac{k \pi}{N}} \) 然后利用这些极点构建系统函数的分母。 4. **去归一化过程**：将归一化系统函数转换为实际的系统函数`Ha(s)`，需要进行频率变换。这里，`Ωc`表示归一化截止频率，对应于题目中的`fp`。因此，将归一化的极点替换为实际频率下的极点，可以得到实际滤波器的系统函数`Ha(s)`。 5. **系统函数Ha(s)**：在本例中，`Ωc`等于2π×6×103 rad/s，因此可以将归一化系统函数`G(p)`的极点转换为`s`域中的极点，并构建实际滤波器的系统函数。完成这一转换后，`Ha(s)`能够反映滤波器在实际信号处理中的行为。 设计一个满足特定要求的数字滤波器是一个涉及多个步骤的过程，包括确定滤波器类型、计算阶数、构建归一化系统函数以及进行频率变换。这个过程对于理解和实现数字信号处理中的滤波器至关重要，也是深入学习数字信号处理课程的学生必须掌握的基本技能。通过解决此类问题，学生不仅可以深化理论理解，还能提高在实际工程问题中应用这些概念的能力。