5.02 TeV Pb-Pb碰撞中J / Ψ前向抑制研究

138 浏览量更新于2024-09-04 收藏 1022KB PDF 举报

"这篇物理论文详细探讨了在CERN大型强子对撞机(LHC)上，使用ALICE探测器在5.02 TeV核子对质心能量的Pb-Pb碰撞以及pp碰撞中J/ψ介子的产生情况。研究中，J/ψ介子通过其衰变成μ子对的方式被重构，分析范围限定在中心速度2.5 < y < 4和横向动量pT < 12 GeV/c。论文呈现了5.02 TeV pp碰撞中J/ψ的包含截面结果，以及核修饰因子(RAA)的结果，后者显示了J/ψ在核碰撞中的抑制现象，并与2.76 TeV Pb-Pb碰撞中的结果进行了比较。此外，还计算了不同能量下的RAA比率，并与统计和动力学模型的预测进行了比较。" 在本文中，ALICE合作组对5.02 TeV的Pb-Pb碰撞和pp碰撞中的J/ψ介子产生进行了深入研究，这是高能粒子物理学的一个重要领域，因为它涉及到夸克-胶子等离子体(QGP)的形成和性质。J/ψ介子，作为重夸克对的束缚态，其在核碰撞中的抑制可以作为QGP存在的直接证据，因为高温高密度的环境可以使得重夸克对解离。测量的RAA值显示，J/ψ介子在Pb-Pb碰撞中受到了显著的抑制，这一发现证实了早期在2.76 TeV能量下的研究结果，表明了在更高等能量的核碰撞中，QGP的形成对重味夸克的产生有显著影响。通过比较两个能量点的RAA比率，研究者可以进一步理解QGP的性质及其随能量变化的行为。在中心度为0到10%的最重叠事件中，RAA的数值为1.17±0.04（统计误差）±0.20（系统误差），在2<pT<6 GeV/c的范围内，随着碰撞能量的增加，RAA显示出轻微增长。这可能是由于在更高的能量下，QGP的寿命和体积增加，导致J/ψ的生存概率有所降低。理论模型在实验数据的不确定范围内对这些测量结果进行了定性描述，但没有完全定量吻合。这表明，尽管我们对QGP的理解已经取得了进展，但仍需要更精细的模型来精确解释这些观测结果。未来的研究将进一步细化这些分析，以期更深入地理解QGP的动态行为和重味夸克的产生机制。

214 ALICE Collaboration / Physics Letters B 766 (2017) 212–224

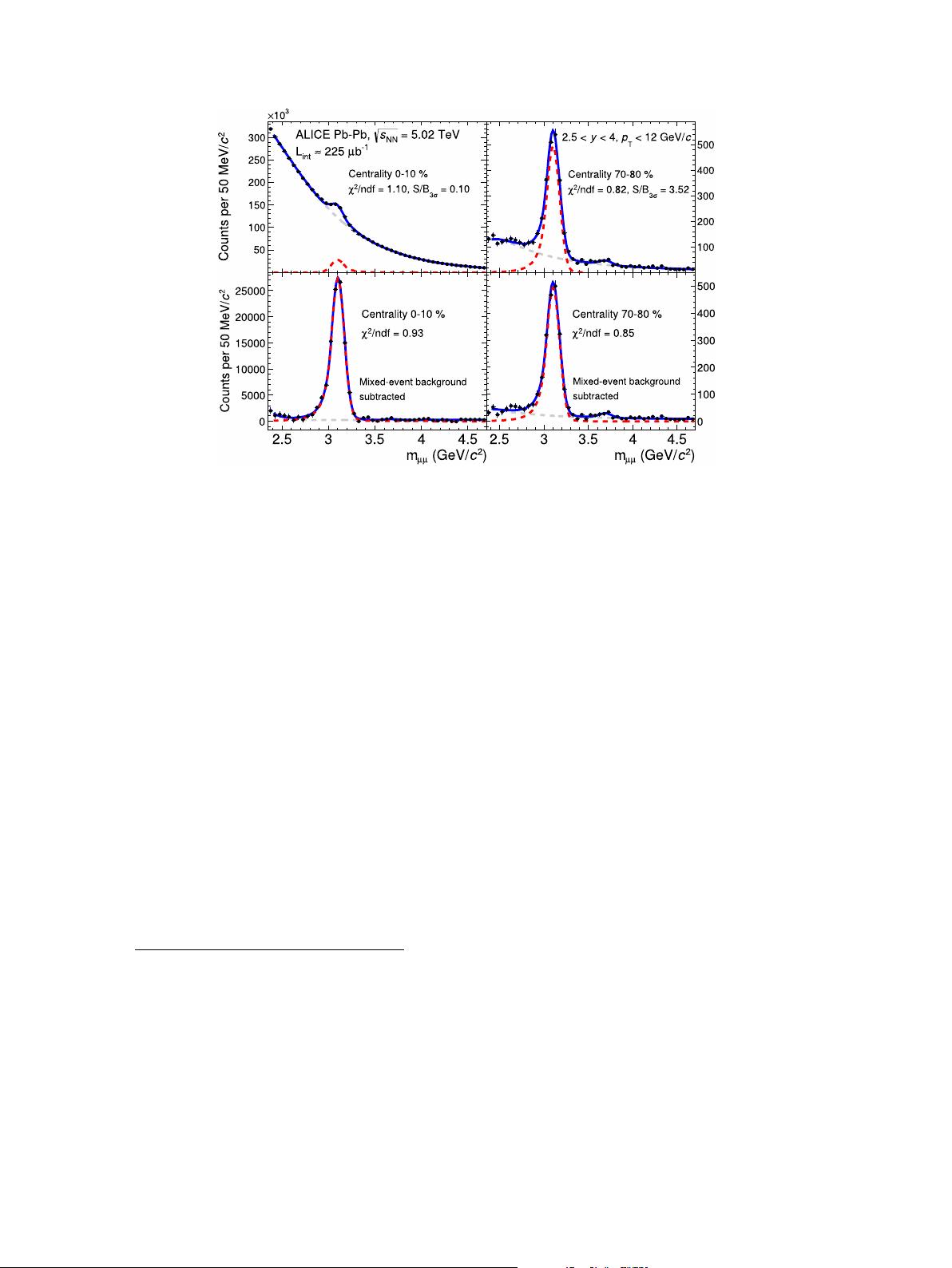
Fig. 1. (Colour online.) Invariant mass distributions of US dimuons with 2.5 < y < 4and p

< 12 GeV/c. The top (bottom) row shows the distribution before (after) background

subtraction with the event-mixing technique. The left panels correspond to the most central events (0–10%) while the right panels to a peripheral (70–80%) centrality range.

The ﬁt curves shown in blue represent the sum of the signal and background shapes, while the red lines correspond to the J/ψ signal and the grey ones to the background.

dimuon continuum component is still present and was ﬁtted us-

ing

the sum of two exponentials. Several ﬁtting sub-ranges, within

the interval 2 < m

μμ

< 5GeV/c

, were used for both signal ex-

traction

procedures.

Fig. 1 sho

ws examples of ﬁts to the US dimuon invariant mass

distributions with and without background subtraction using the

event-mixing technique, for different selections in centrality. The

raw J/ψ yield in each centrality or p

interval was determined

as the average of the results obtained with the two ﬁtting ap-

proaches,

the various parameterisations of signal and background

and the different ﬁtting ranges, while the corresponding systematic

uncertainties were deﬁned as the RMS of these results. A further

contribution to the systematic uncertainty was estimated by using

a different set of resonance tails obtained using in the MC simu-

lation

a different particle transport model (GEANT4 [37] instead of

GEANT3 [38]). The total number of J/ψ , integrated over centrality,

and y, is N

J/ψ

= 2.77 ±0.02(stat) ±0.05(syst) ·10

. The system-

atic

uncertainty ranges from 1.6% to 2.8% as a function of centrality

and from 1.2% to 3.1% as a function of p

The

nuclear modiﬁcation factor, as a function of the centrality

class i of the collision and for the J/ψ transverse-momentum in-

terval

p

, is calculated as

(p

) =

/ψ

(p

)

J/ψ→μ

−

Aε

(p

)T

σ

/ψ

(p

)

(1)

where N

/ψ

(p

) is the number of extracted J/ψ in a given cen-

trality

and p

range, BR

J/ψ→μ

−

= 5.96 ± 0.03% is the branching

ratio of the dimuon decay channel [39], N

is the number of

equivalent minimum-bias events, Aε

(p

) is the product of the

detector acceptance times the reconstruction eﬃciency, T

 is

the average of the nuclear overlap function, and σ

/ψ

(p

) is the

inclusive J/ψ cross section for pp collisions at the same energy and

in the same kinematic range as the Pb–Pb data.

The

Aε values were determined from MC simulations, with the

generated p

and y distributions for the J/ψ adjusted on data,

and separately tuned for each centrality class using an iterative

approach. Unpolarised J/ψ production was assumed [21]. For the

tracking chambers, the time-dependent status of each electronic

channel during the data taking period was taken into account as

well as the misalignment of the detection elements. The eﬃcien-

cies

of the muon trigger chambers were determined from data and

were then applied in the simulations. Finally, the dependence of

the eﬃciency on the detector occupancy was taken into account

by embedding MC-generated J/ψ into real minimum-bias Pb–Pb

events.

For

J/ψ produced within 2.5 < y < 4 and p

< 12 GeV/c, in

0–90% most central collisions, the Aε value is 0.136 ± 0.007(syst).

A relative decrease of the eﬃciency by 14% was observed when

going from peripheral to central collisions. As a function of p

Aε has a minimum value of about 0.12 at p

≈ 1.5GeV/c, and

then steadily increases up to about 0.4 at the upper end of the

considered range. The following sources of systematic uncertainty

on Aε were considered. A ﬁrst contribution of 2% due to the in-

put

MC p

and y distributions was estimated by (i) varying the

input shapes that were tuned on data within their statistical un-

certainties

and (ii) taking into account the effect of possible p

− y

correlations

by comparing, as a function of centrality, the Aε val-

ues

with the corresponding result of a 2-D acceptance calculation

in classes of p

and y. A second contribution comes from the

tracking eﬃciency and it was estimated by comparing the single-

muon

tracking eﬃciency values obtained, in MC and data, with

a procedure that exploits the redundancy of the tracking-chamber

information [21]. A 3% systematic uncertainty on the dimuon track-

ing

eﬃciency is obtained and is approximately constant as a func-

tion

of centrality and kinematics. The systematic uncertainty on

the dimuon trigger eﬃciency represents the third contribution and

it has two origins: the intrinsic eﬃciencies of the muon trigger

chambers and the response of the trigger algorithm. The ﬁrst one

was determined from the uncertainties on the trigger chamber ef-

ﬁciencies

measured from data and applied to simulations and it

amounts to 1.5%. The second one was estimated by comparing the

dependence, at the single-muon level, of the trigger response

function between data and MC and it varies between 0.2% and 4.6%

as a function of p

. Combining the two sources, a systematic un-

certainty

ranging from 1.5% to 4.8% as a function of the J/ψ p

obtained. Finally, there is a 1% contribution related to the choice

剩余12页未读，继续阅读

weixin_38599430

粉丝: 0
资源: 886

5.02 TeV Pb-Pb碰撞中J / Ψ前向抑制研究

J / Ïˆ抑制在sNN = 2.76 TeV时Pb–Pb碰撞中的中心性，速度和横向动量依赖性

Ï•-前向速度的介子生产在sNN = 5.02 TeV处的p–Pb碰撞中和在s = 2.76 TeV处的pp碰撞中

相干Ïˆ（2S）照片生产在sNN = 2.76 TeV的超外围Pb Pb碰撞中

在s = 7 TeV的pp碰撞中测量比率B（Bs0→J / Ïˆf0（980））/ B（Bs0†J / ÏˆÏ•（1020））

在sNN = 2.76 TeV的Pb-Pb碰撞中的H› 3和Hâ€›β3生产

J / Ïˆ家族中4.26 GeV周围缺少更高的富氢原子的预测

在sNN = 200 GeV时在d + Au和Au + Au碰撞中抑制Ï生产

在s = 8 TeV的质子-质子碰撞中产生π0和η介子

在带有b标签的射流的最终状态下，在s = 8TeV的pp碰撞中测量pp碰撞中WZ和ZZ产生

使用ATLAS探测器在s = 7 TeV的质子-质子碰撞中测量唯一的γ-α-β-++-β产生

最新资源