Python递归函数实现分形树绘制
14 浏览量
更新于2024-08-28
收藏 303KB PDF 举报
"本文将介绍递归函数的概念和应用,以Python编程语言为载体,通过绘制分形树作为示例,深入浅出地讲解递归的原理和实践。"
递归函数是计算机科学中一种重要的编程技巧,它指的是在函数定义中调用自身的过程。这种调用方式使得函数能够解决复杂问题,特别是那些具有自相似结构的问题。在Python中,递归函数通过设置终止条件来避免无限循环,并逐步解决问题。例如,函数`f(x)`调用自身形成`f(f(x))`,这便是递归调用的一个实例。
在递归调用过程中,每次函数被调用,其参数会被存储并形成一个新的调用栈。当达到终止条件时,函数会逐层返回结果,直到最初的调用结束。如果没有正确设定终止条件,递归函数可能会陷入无限循环,导致程序崩溃。
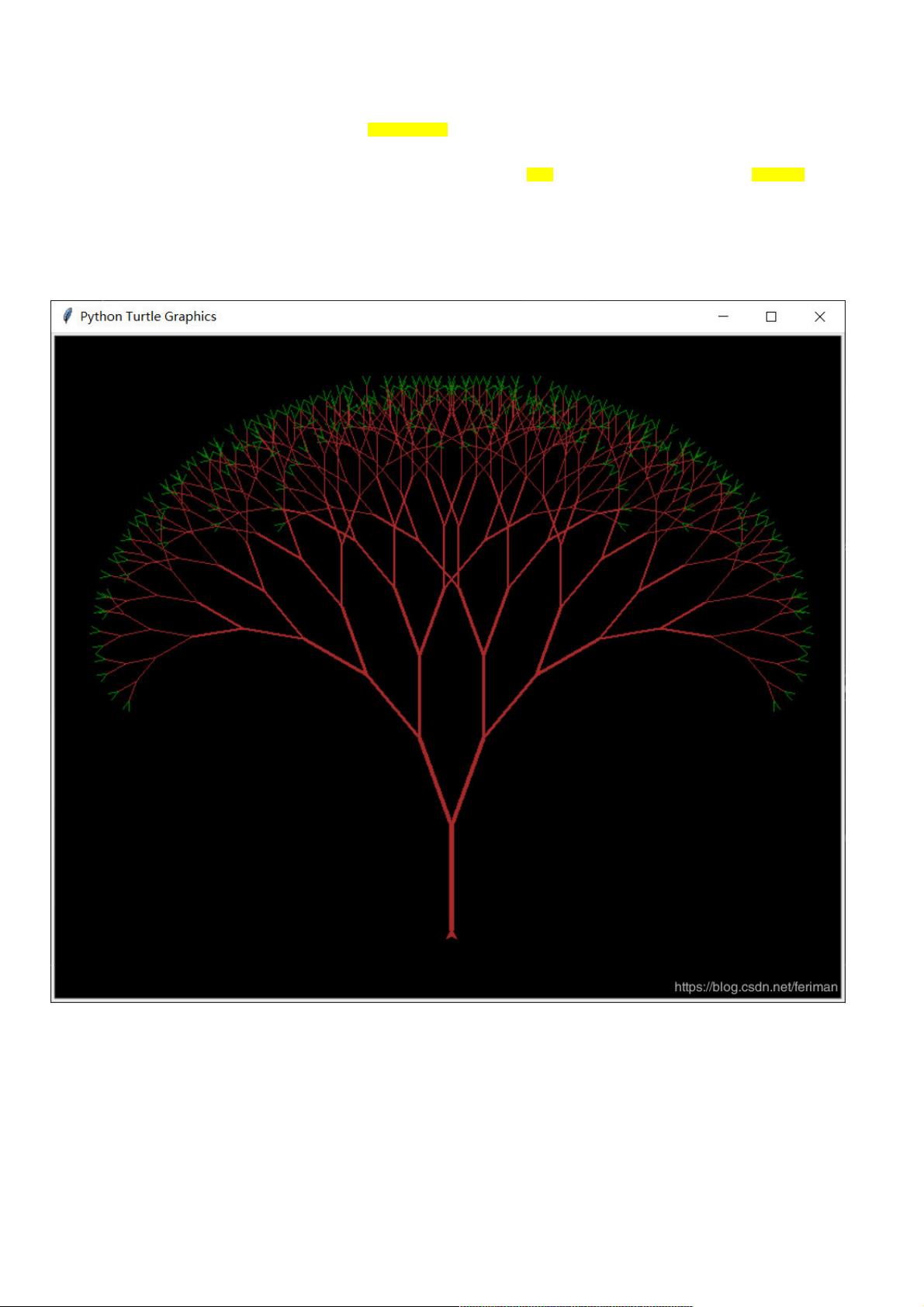
分形是一种几何形状,具有自相似性,即无论在哪个尺度上观察,它们都保持相似的结构。分形树是分形几何学的一个经典示例,其分支模式呈现出层级结构,每一层都是上一层的缩小版。在编程中,我们可以通过递归函数来模拟这种结构。
在Python中,`turtle`模块是一个用于绘图的库,它可以方便地绘制出分形树。虽然这里不再详细介绍`turtle`的用法,但可以知道它提供了基本的绘图操作,如移动、转向等,这些操作非常适合用于绘制复杂的图形,比如分形树。
为了画出分形树,我们可以定义一个递归函数,该函数接受两个参数,例如当前的长度`x`和角度`y`,表示当前分支的长度和角度。函数内部首先执行一定的绘图操作(如向前移动`x`距离),然后根据角度进行转向,接着递归调用自身,但每次调用时会调整参数(如减小长度`x`或改变角度`y`)。这样,每次递归都将创建一个更小的分支,直到达到某个最小长度或者达到指定的分支深度,此时终止条件被触发,递归停止。
在实际编写代码时,需要注意控制递归深度,防止栈溢出。递归深度通常与系统的限制和问题的规模有关,过度的递归可能导致程序崩溃。此外,递归函数的效率较低,因为每次调用都会增加栈的开销,所以对于大规模数据处理,可能需要考虑其他非递归算法。
总结来说,递归函数在解决分形树这样的自相似问题时,能展现出强大的能力。通过理解递归的概念、终止条件的设定以及如何利用递归模拟分形结构,我们可以在Python中创建出美观的分形图形。递归不仅在计算机科学中有广泛的应用,也是理解和解决复杂问题的重要思维方式。
113 浏览量
118 浏览量
点击了解资源详情
点击了解资源详情
143 浏览量
点击了解资源详情
点击了解资源详情
weixin_38686677
- 粉丝: 2
最新资源
- VB6程序实现鼠标操作模拟与自动点击
- 局域网内socket编程实现文件传输教程
- EmguCV人脸对比识别技术实践指南
- Oracle试题及答案下载:1Z0-045考试攻略
- 深入探索BankAPI:Elixir语言开发的银行服务接口
- win7 64位系统汇编环境搭建指南
- HTML5+JS全屏单页问卷模板,逐页填写实用问卷
- 打造类谷歌百度搜索提示效果的jQuery插件
- 高效 Dotnet Dumper:解锁更多DLL文件脱壳能力
- Flac3D软件操作与示例教程详解
- starlight.js: jQuery实现动态背景特效插件
- 剪刀石头布游戏开发教程
- 模电基础课后答案全解析:第1-6章详尽版
- RTM低频假象去除与空间域Laplace滤波技术
- C++实现学生成绩管理系统及课程设计题目
- 响应式滚动布局单页模板实现技术解析