研究生数值分析：地球表面积计算与牛顿迭代法应用

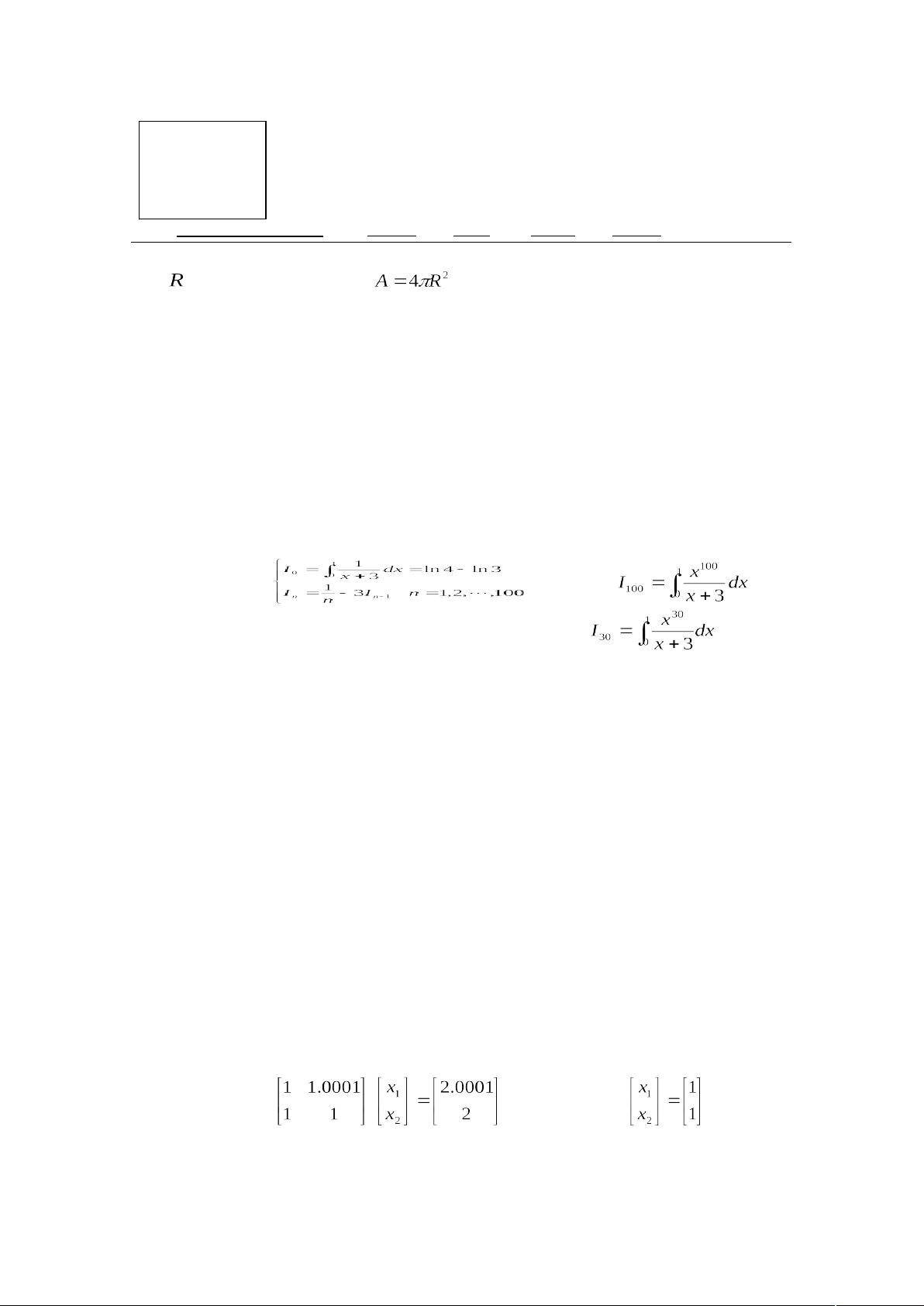
在2006-2007学年第1学期的南京农业大学研究生数值分析课程中，学生将面临一系列关于数值计算和理论分析的问题。课程内容涵盖了多个关键知识点： 1. 地球表面积计算：题目要求分析利用公式 [pic] 计算地球表面积时为何无法得到真实值。这涉及球体体积和表面积的计算，实际上公式中的常数π和地球真实半径会导致理论计算与实际值有偏差，因为该公式适用于理想化的球体模型，而地球并非完美的球形。 2. 定积分问题：编程计算中出现负数，可能是因为数值方法的精度问题或者在处理特殊点（如积分区间端点）时的数值稳定性不足。解决方案可能包括提高计算精度、使用数值积分方法（如辛普森法则）或者改变积分区间处理方式。 3. 方程组求解与残差分析：对于方程组 [pic]，虽然初始近似值 [pic] 虽然看起来更接近准确解，但残差分析显示其效果不如 [pic]。需要计算 [pic] 和 [pic] 的条件数来评估矩阵的稀疏性和线性系统的敏感性，解释为什么残差表现不同。 4. 分段低次插值多项式近似：优点是简单易用，适合处理简单函数，但对复杂函数或光滑度较差的函数可能效果不佳。改进方法可以是使用更高阶的插值多项式或局部调整插值节点以提高精度。 5. 多项式插值与最小二乘法：多项式插值侧重于精确通过给定点，但可能不适于光滑度变化大的函数。最小二乘法则是寻找最能逼近数据点的曲线，但不强制通过所有点，适合噪声较多的数据。选择哪种方法取决于具体应用的需求，如函数精确度、数据特性等。 6. 牛顿迭代法：学生需证明方程 [pic] 的牛顿迭代法的局部收敛性，并计算初始近似值 [pic] 的迭代结果。这涉及到迭代过程的理论分析和实际计算步骤。 7. Gauss-Seidel迭代法：题目要求写出并验证Gauss-Seidel方法应用于方程组 [pic] 的收敛性。这是矩阵代数和迭代解法的实际应用。 8. 二次牛顿插值：利用给定的数据，学生需构建二次多项式近似 [pic] 并估计误差，涉及插值理论和误差分析。 9. 超定方程组的最小二乘解：利用最小二乘原理求解给定方程组，这是一个线性代数中的核心问题，需要理解最小化残平方和的概念。 总体来说，这门课程要求学生深入理解数值分析的基本概念和技术，包括误差分析、迭代方法、插值理论以及线性方程组的求解，同时结合具体实例进行实践操作和问题解决。