方格取数路径优化算法：最大和求解

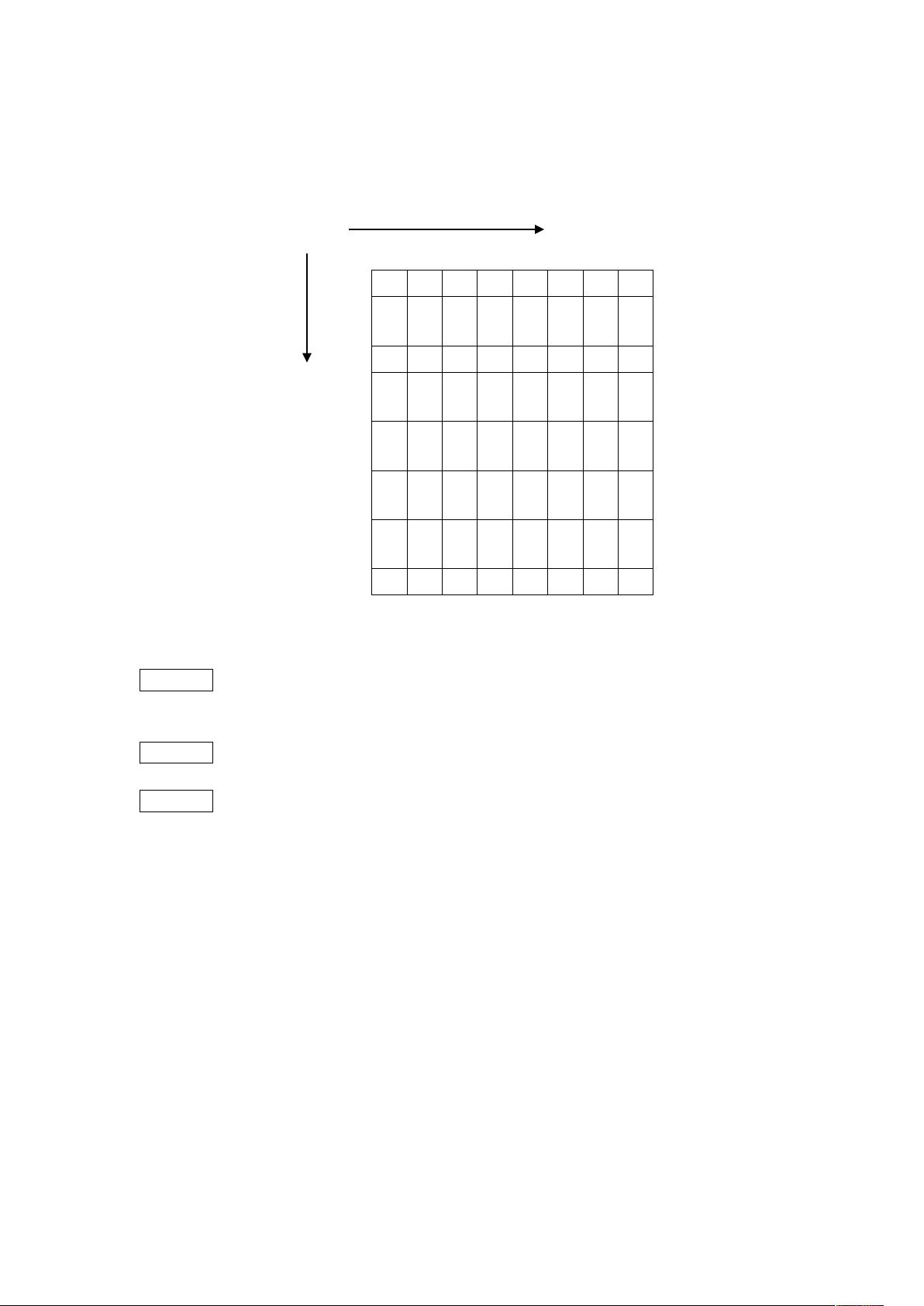
方格取数系列算法分析 方格取数是一个经典的问题，涉及在一个给定的N×N方格图（N≤8）中寻找路径，其中包含正整数和0。玩家从左上角的A点出发，按照向下或向右的规则移动，直到到达右下角的B点。目标是在两条路径上取走的数字之和达到最大。这个问题源于1997年国际信息学奥林匹克的障碍物探测器竞赛题目，但在此简化版本中，只考虑两次路径。 问题的关键在于设计动态规划策略来解决。首先，定义一个二维数组`data`，存储每个位置的数值，同时为了处理边界条件，添加了零行和零列。数组`sum`用于记录从A点到每个位置所能取得的最大数之和。初始化时，`sum`的零行和零列设置为0。 对于每个位置`(i, j)`（非边界），算法计算两种可能路径的价值：一种是通过上一个位置（`sum[i-1, j]`），另一种是通过左侧位置（`sum[i, j-1]`）。然后选择较大者加上当前位置的数值`data[i, j]`更新`sum[i, j]`。遍历结束后，`sum`数组不仅包含了最大路径和，还蕴含了路径信息，可以通过回溯找到最优路径。 具体步骤如下： 1. 初始化`sum`数组，添加零行和零列，并设置值为0。 2. 遍历`data`矩阵： - 对于每个内部位置 `(i, j)`： - 比较`sum[i-1, j]` 和 `sum[i, j-1]` 的值。 - 如果`sum[i-1, j]`较大，则`sum[i, j]`更新为`sum[i-1, j] + data[i, j]`。 - 否则，`sum[i, j]` 更新为`sum[i, j-1] + data[i, j]`。 3. 最终`sum[N-1, N-1]`即为所求的两条路径上最大数字之和。 4. 回溯路径：根据`sum`数组的值，从`N-1, N-1`开始，每次选择上一步中使和增加较多的那个方向，直到回到A点。 总结来说，方格取数问题利用动态规划的思想，通过迭代求解每个位置的最大路径和，再通过倒推确定最优路径，最终求得两条路径上数字之和的最大值。这是一个典型的应用了数学优化方法和递归思想的算法问题。