人工神经网络模型解析：从MP模型到BP网络

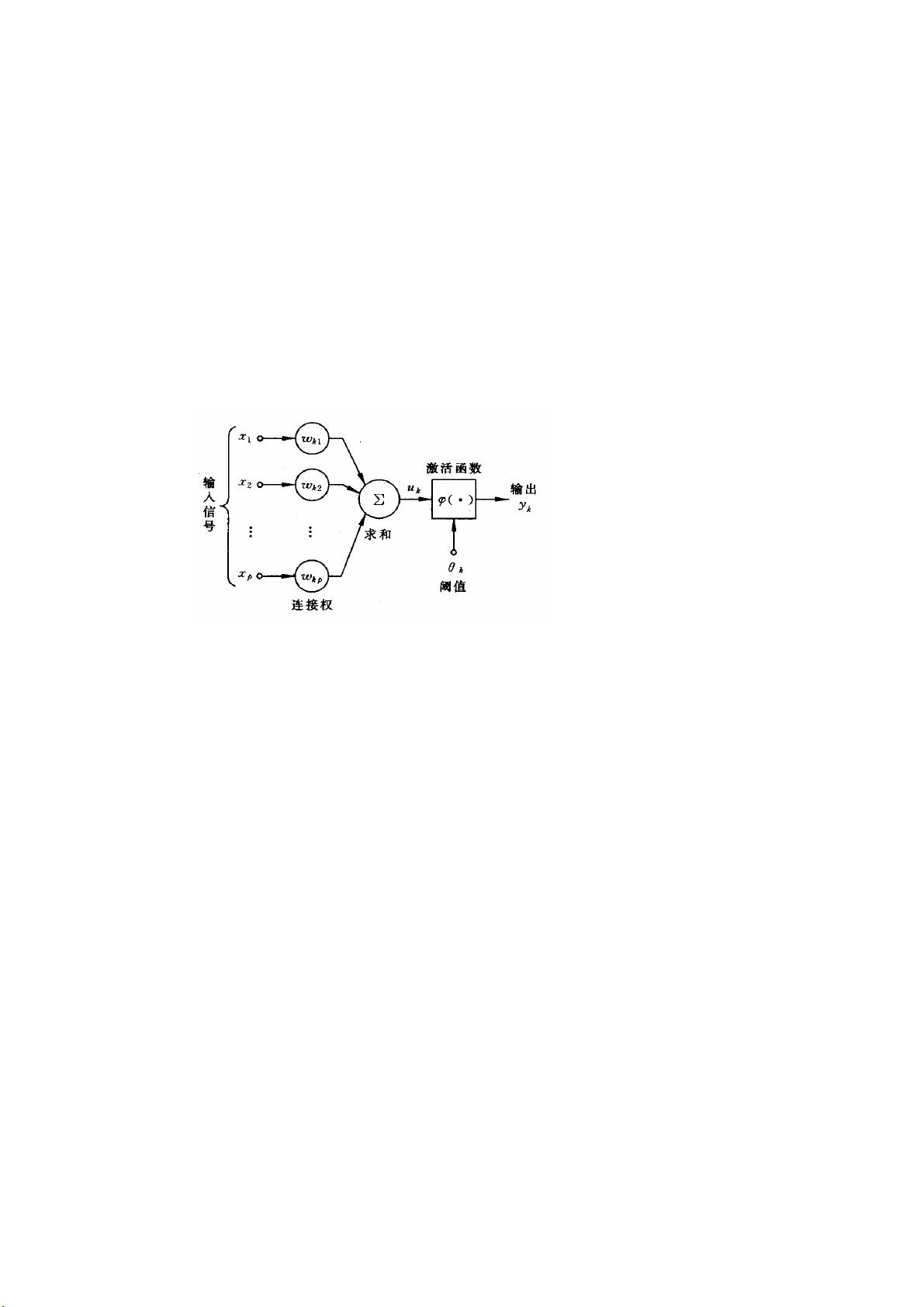
"神经网络模型是基于现代神经科学的数学模型，用以模拟人脑的结构和功能。这种模型由MP模型发展而来，经过50多年的发展，在20世纪80年代取得了重大突破，成为多学科交叉的研究领域。神经网络在模式识别、图像处理、智能控制等领域有广泛应用，包括感知机、Hopfield网络、Boltzmann机、自适应共振理论和反向传播网络（BP）等多种模型。本文主要讨论基础的人工神经元模型和学习算法。 1.1 人工神经元模型 人工神经元是神经网络的基本构建单元，由三个核心部分组成： 1. 连接：代表生物神经元的突触，权重表示连接强度，正权重表示激活，负权重表示抑制。 2. 求和单元：计算所有输入信号的加权和，形成线性组合。 3. 非线性激活函数：进行非线性映射，限制输出幅度在特定范围内，通常在-1到1之间。此外，还有阈值（或偏置）。 数学上，神经元的运算可以用以下公式表示： \[ \sum_{j=1}^{L} w_{kj} x_j = u_k \] \[ u_k - \theta_k = v_k \] \[ y_k = \phi(v_k) \] 其中，\( p \) 是输入信号的维数，\( x_1, x_2, ..., x_L \) 是输入信号，\( w_{kj} \) 是神经元k到输入j的权重，\( u_k \) 是线性组合的结果，\( \theta_k \) 是阈值，\( \phi \) 是激活函数，\( y_k \) 是神经元k的输出。 当阈值包含在内时，可以增加一维输入，例如： \[ \sum_{j=0}^{L} w_{kj} x_j = u_k \] \[ u_k - \theta_k = y_k \] 这里的 \( x_0 \) 通常设置为1（或-1），对应的权重 \( w_{k0} \) 为阈值 \( \theta_k \)（或 \( b_k \)）。 1.2 激活函数 激活函数是神经网络非线性的重要来源，常见的激活函数包括sigmoid、ReLU、tanh等。它们将神经元的线性组合结果转换为非线性输出，从而增加模型的表达能力。例如，sigmoid函数 \( \phi(x) = \frac{1}{1+e^{-x}} \) 能够将输入映射到(0,1)之间，而ReLU函数 \( \phi(x) = \max(0, x) \) 则将负值截断为0，正值保持不变。 神经网络通过调整权重和阈值，使用学习算法（如梯度下降、反向传播等）来优化模型，以更好地拟合数据并解决复杂问题。这些模型和算法是深度学习技术的基础，对于理解和实现各种现代AI应用至关重要。"