《信号与系统》详解：频域分析与傅立叶变换

"《信号与系统》的答案包含详细的例题和知识点解析，涵盖连续时间信号与系统的频域分析，重点讨论了频谱、傅立叶变换、系统响应和频率响应等概念。" 本文将深入探讨《信号与系统》中关于连续时间信号与系统的频域分析相关知识点，主要包括信号的正交分解、周期信号的傅立叶级数、指数形式的傅里叶级数以及周期信号的功率谱。 3.4.1 信号的正交分解 在信号处理中，正交分解是将复杂信号分解为一组正交基函数的线性组合。如果一个函数集满足正交条件，即它们的点积为零，那么这个集合被称为正交函数集。对于完备正交函数集，任何在该区间内的信号都可以被精确表示为这些函数的线性组合，通过计算每个基函数的标量系数来获得。 3.4.2 周期信号的傅立叶级数 傅立叶级数是将周期信号分解为不同频率的正弦和余弦函数的和。三角形式的傅立叶级数展示了信号如何由直流分量、基波和各次谐波组成。指数形式的傅立叶级数则是另一种表示方式，更加抽象，其中复指数函数提供了幅度和相位信息。通过绘制幅度频谱图和相位频谱图，可以直观地理解信号的频率成分。 3.4.3 周期信号的功率谱 功率谱描述了周期信号的功率分布，它是傅立叶级数中各频率分量的平方与频率的乘积。帕塞瓦尔关系式揭示了周期信号的平均功率与其离散谱之间的关系，这对于理解和分析信号的能量分布至关重要。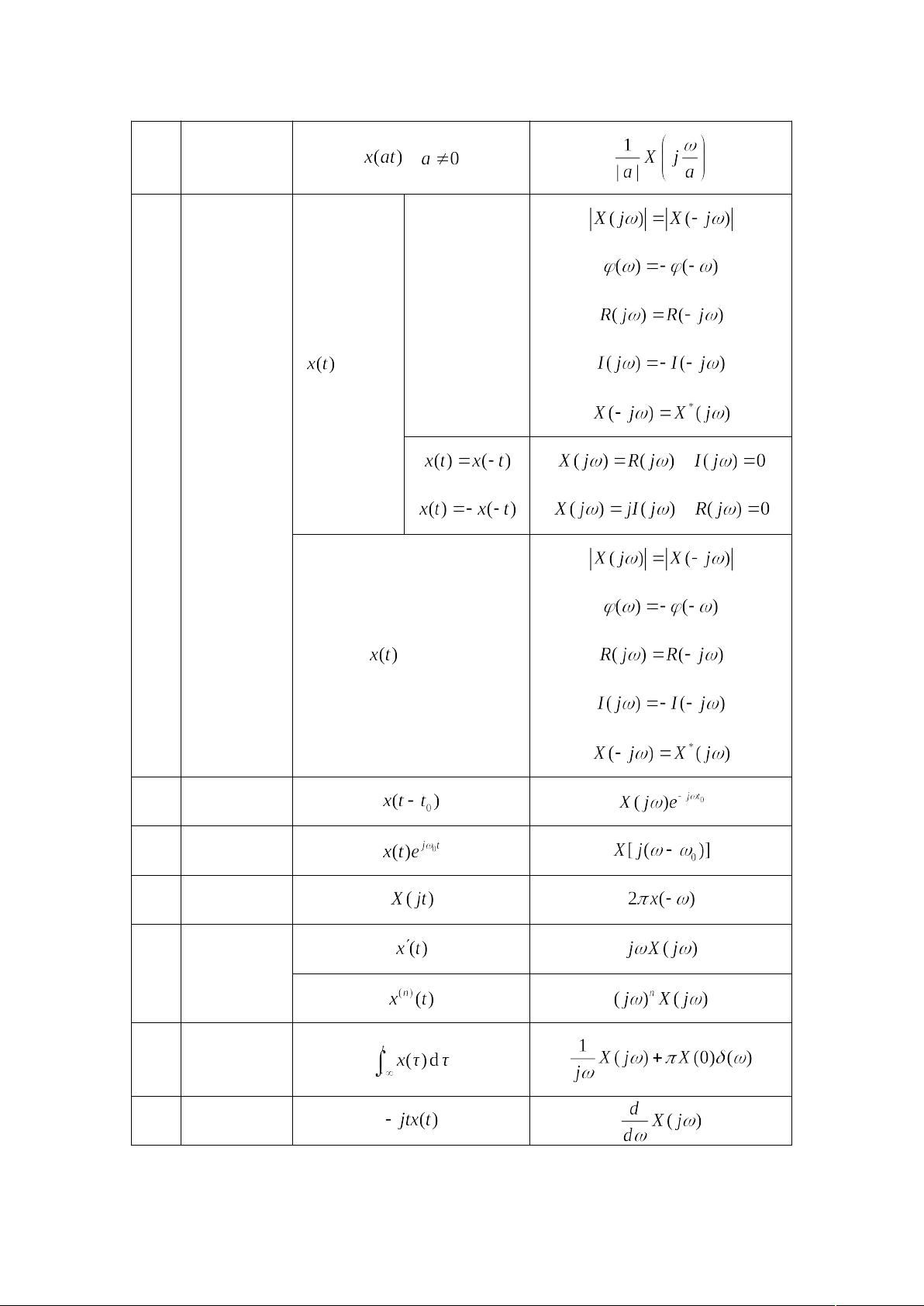 在《信号与系统》的学习中，理解和掌握这些概念对于分析系统的响应、设计滤波器以及进行通信信号的处理极其关键。傅立叶变换作为非周期信号的频域描述工具，其性质和应用广泛，包括卷积、微分和积分等操作。而系统的频率响应则反映了系统对不同频率输入的响应特性，这对于理解系统无失真传输和理想滤波的原理至关重要。 总结起来，《信号与系统》的答案提供了一个全面的平台，帮助学习者深入理解信号的频域分析，包括正交分解的基础、傅立叶级数的计算以及功率谱的解析，这些都是信号处理和系统分析中的核心概念。通过学习这部分内容，可以提升在实际工程问题中的分析和解决能力。