拉普拉斯矩阵与GCN：从一维热传导到图神经网络

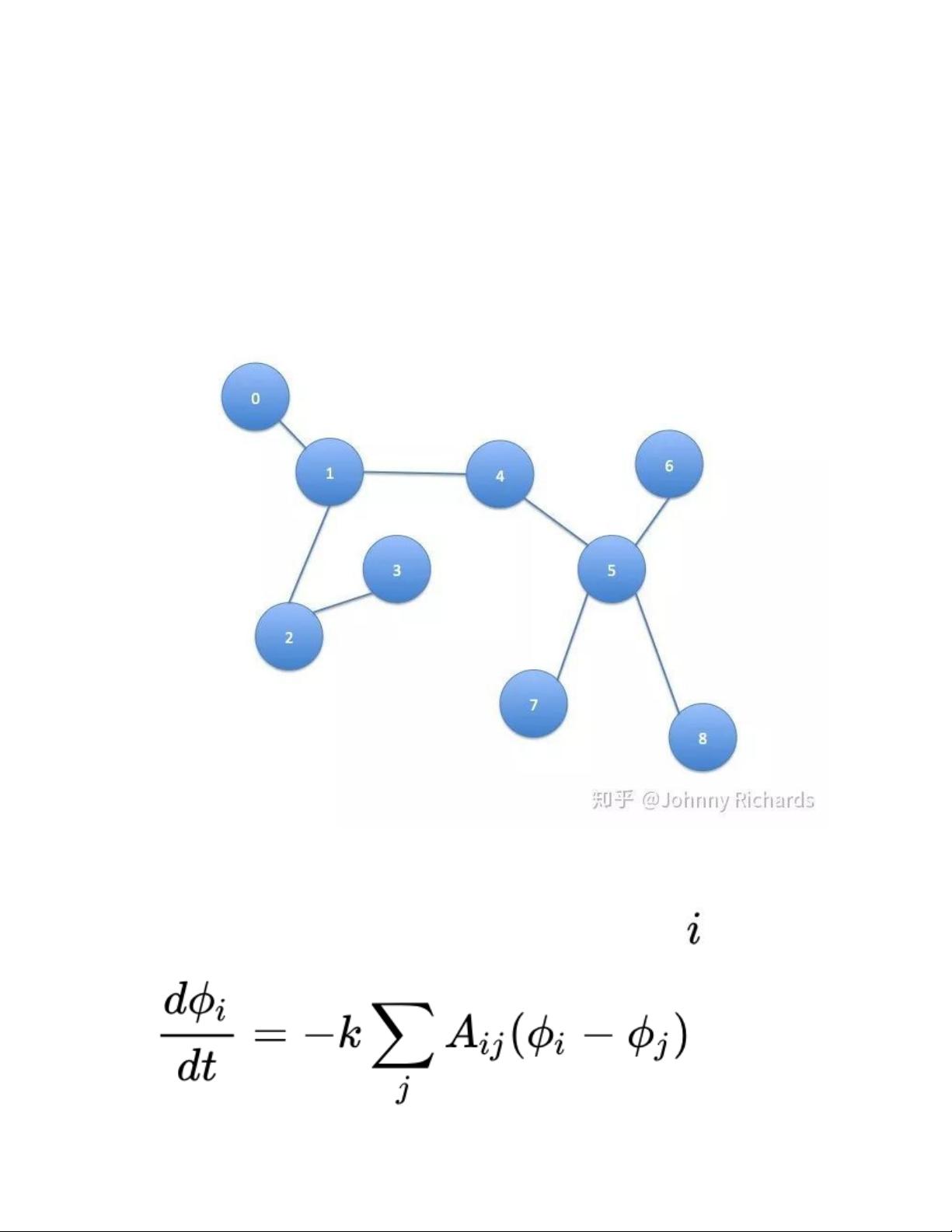
"本文从Laplacian矩阵出发，探讨了其在理解图卷积网络（GCN）中的作用。首先介绍了热传导的一维模型，通过离散化空间，将温度传播转化为单元之间的热量交换，进而引出一维空间中的热传导方程，即一阶导数的负值表示温度变化率。在高维空间中，这一概念演变为拉普拉斯算子，它是二阶导数的推广，衡量的是点周围环境的温度分布。" 在图论中，拉普拉斯矩阵进一步与图的结构相关联。在图上构建热传导模型时，每个节点代表一个单元，节点之间的边代表它们之间的相互作用。在图的热传导过程中，热量的传递不再是简单的基于距离的传播，而是依赖于节点之间的连接关系。图的拉普拉斯矩阵正是用来描述这种拓扑结构下的信息传递或能量流动。 拉普拉斯矩阵通常定义为 \( L=D-A \)，其中 \( D \) 是度矩阵，对角线元素为节点的度（即与之相连的边的数量），\( A \) 是邻接矩阵，表示节点间边的存在。在无向图中，拉普拉斯矩阵是对称的，表示热量在节点间的传递是双向的。而在有向图中，可能需要使用归一化的拉普拉斯矩阵或随机游走拉普拉斯矩阵。 图卷积网络（GCN）利用拉普拉斯矩阵的性质进行信息传播和特征学习。GCN每一层的计算涉及到节点特征向量的更新，这与拉普拉斯矩阵的谱分解密切相关。通过拉普拉斯矩阵，GCN能够捕捉到节点的局部邻域信息，并进行平滑操作，使得相邻节点的特征趋于相似。这与热传导过程中温度逐渐趋于均衡的过程相类似。 GCN的层级结构允许信息在不同层次的邻居之间传播，从而实现非线性特征的抽取。每一层的节点特征向量更新可以表示为： \[ H^{(l+1)} = \sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}) \] 这里，\( H^{(l)} \) 表示第 \( l \) 层的节点特征矩阵，\( \tilde{A} \) 是加入自环的邻接矩阵，\( \tilde{D} \) 是对应的度矩阵，\( W^{(l)} \) 是权重矩阵，\( \sigma \) 是激活函数。 总结来说，拉普拉斯矩阵是连接几何空间中热传导理论与图数据处理的关键工具。在图卷积网络中，它用于捕获图的拓扑结构，驱动特征在节点间的传播和融合，是GCN能够有效处理复杂网络数据的基础。通过对拉普拉斯矩阵的理解，我们可以深入认识GCN如何在图数据上进行有效的信息处理和学习。