浮点数编码表示详解

"浮点数的编码表示.pdf" 在计算机科学中，浮点数是一种用于表示实数的数据类型，尤其适用于科学计算和工程应用。浮点数的编码表示是计算机内部存储和处理这些数值的方式。在C语言中，常见的浮点数类型包括单精度浮点数（float）、双精度浮点数（double）和扩展精度浮点数（long double），它们分别占用32位、64位和80/96位。不同类型的浮点数有不同的精度和表示范围。 浮点数由两部分组成：尾数（mantissa）和指数（exponent）。尾数表示小数部分，指数则指示小数点的位置。在科学记数法中，一个数可以写成`mantissa * base^exponent`的形式，其中base是基数，通常为2（二进制系统）。 规格化形式（Normalized form）是浮点数的一种标准表示，确保小数点前总有一个非零数字。例如，1/1,000,000,000可以用规格化形式1.0x10^-9表示，也可以用非规格化形式0.1x10^-8或10.0x10^-10表示，尽管它们代表相同的值。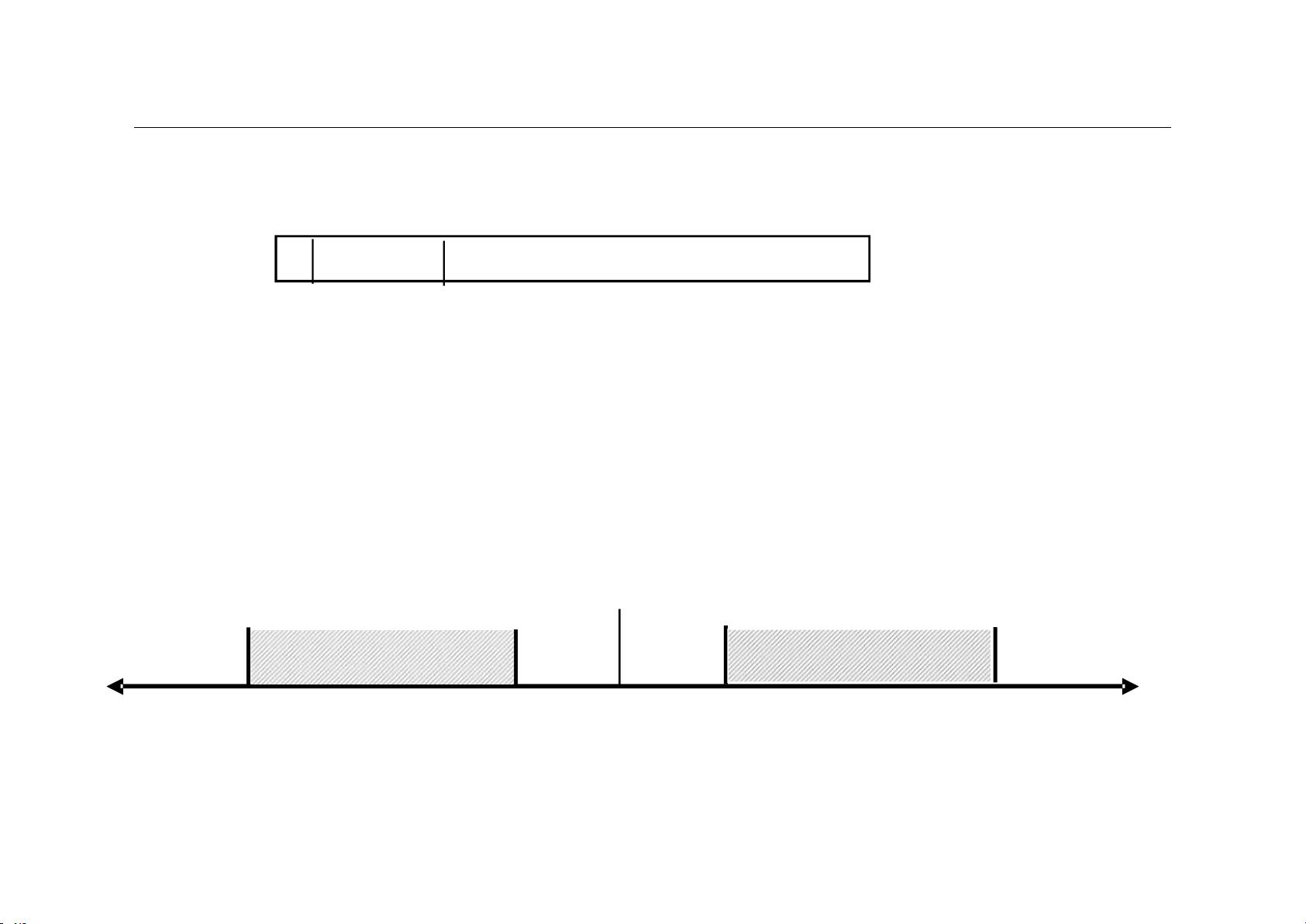 在二进制浮点数中，尾数和指数分别被编码。对于32位浮点数格式，如IEEE 754单精度格式，它包含1个符号位（S），8位指数（E，使用移码表示，偏置常数为128），以及23位尾数（M）。尾数通常假设小数点后第一位为1，因此这个“1”并不实际存储，从而节省了一个位，使尾数能表示24位的值。 这种编码方式定义了浮点数的表示范围。例如，对于上述32位浮点数格式，最大正数是(1-2^-24) * 2^(127)，最小正数是(1/2) * 2^(-127)。由于原码的对称性，负数的范围是对称的，包括零。零有两种表示：正零和负零。此外，还有下溢（subnormal）区域，用于表示非常接近零但不等于零的数。 浮点数的这种表示方式虽然扩大了数值的表示范围，但同时也导致了数值密度不均匀，某些区域的数值间隔较大，而其他区域则较小。相比于定点数，浮点数之间的间隔不是恒定的，这可能导致精度上的差异和计算误差。 理解浮点数的编码表示对于优化数值计算、理解精度损失以及处理可能的浮点异常（如下溢和上溢）至关重要。在编程时，尤其是在进行数值敏感的计算时，需要考虑到这些因素，以确保结果的准确性和可靠性。