根轨迹法分析自动控制系统

"北工业大学的自动控制原理课程17至24讲，主要讲解了根轨迹法及其在分析系统性能中的应用。" 本文将深入探讨自动控制原理中的根轨迹法，这是控制系统设计和分析中的一个重要工具。根轨迹法是一种研究系统稳定性、动态性能和控制品质的方法，它通过分析闭环极点随开环增益变化的轨迹来揭示系统的行为。 首先，根轨迹是系统闭环极点随着开环增益K从0变到无穷大时在复平面上的轨迹。这些轨迹的形成受到开环零点、开环极点以及K的影响。根轨迹的绘制需要满足模值条件和相角条件，这是确定轨迹形状的关键。模值条件规定了根轨迹的幅值变化，而相角条件则涉及轨迹的转向。 在绘制根轨迹时，有八条基本法则需要遵循。法则5，即渐近线法则，指出根轨迹在某些特定点的渐近行为；法则2涉及根轨迹的分支数、对称性和连续性；法则3说明了实轴上的根轨迹分布；法则4，根之和法则，用于确定根轨迹如何穿过实轴；法则6，分离点法则，定义了根轨迹分支的分离情况；法则7处理根轨迹与虚轴的交点；法则8则涉及根轨迹出射角和入射角的计算。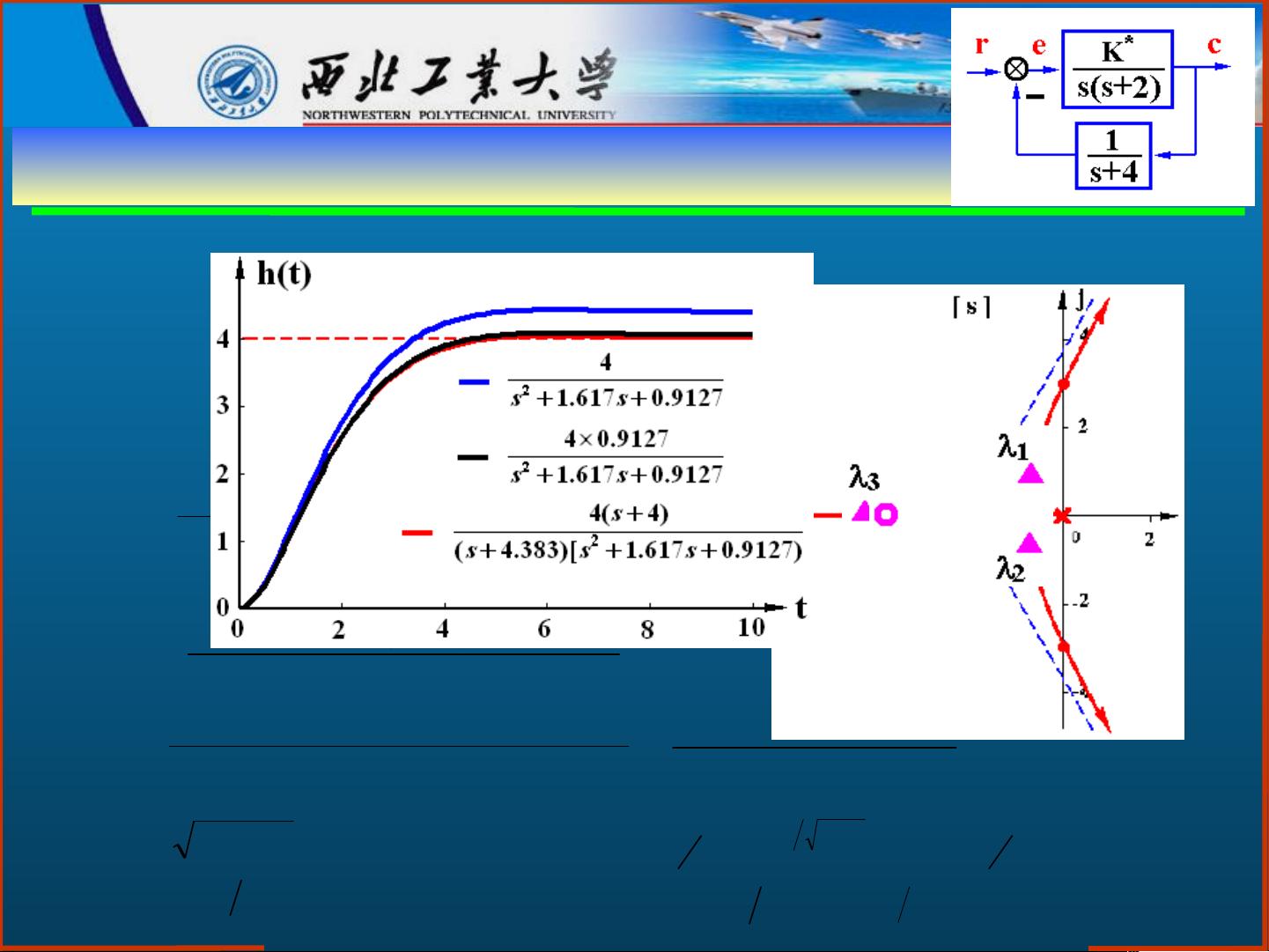 在分析系统性能方面，根轨迹法可以用来确定系统的稳定性范围。例如，可以通过观察根轨迹与虚轴的交点来确定闭环极点的位置，进而评估系统的稳定性和动态响应。欠阻尼状态通常对应于系统具有稳定的负实部闭环极点，这可以通过调整开环增益K来实现。 在实际应用中，我们需要根据题目要求，如例1和例2所示，逐步绘制根轨迹，确定闭环极点和零点的位置，然后利用零点极点法估计系统的性能指标，如上升时间ts、超调量σ%等。通过解方程和比较系数，我们可以找到满足特定条件的K值和闭环极点坐标，从而分析系统的动态响应。 北工业大学自动控制原理课程的这部分内容深入讲解了根轨迹法，它是理解复杂控制系统行为、优化系统性能和设计控制器的基础。通过实例解析，学生能够掌握根轨迹法的实际运用，提升其在控制系统设计中的理论和实践能力。