迭代计算正余弦值推导与FPGA实现总结

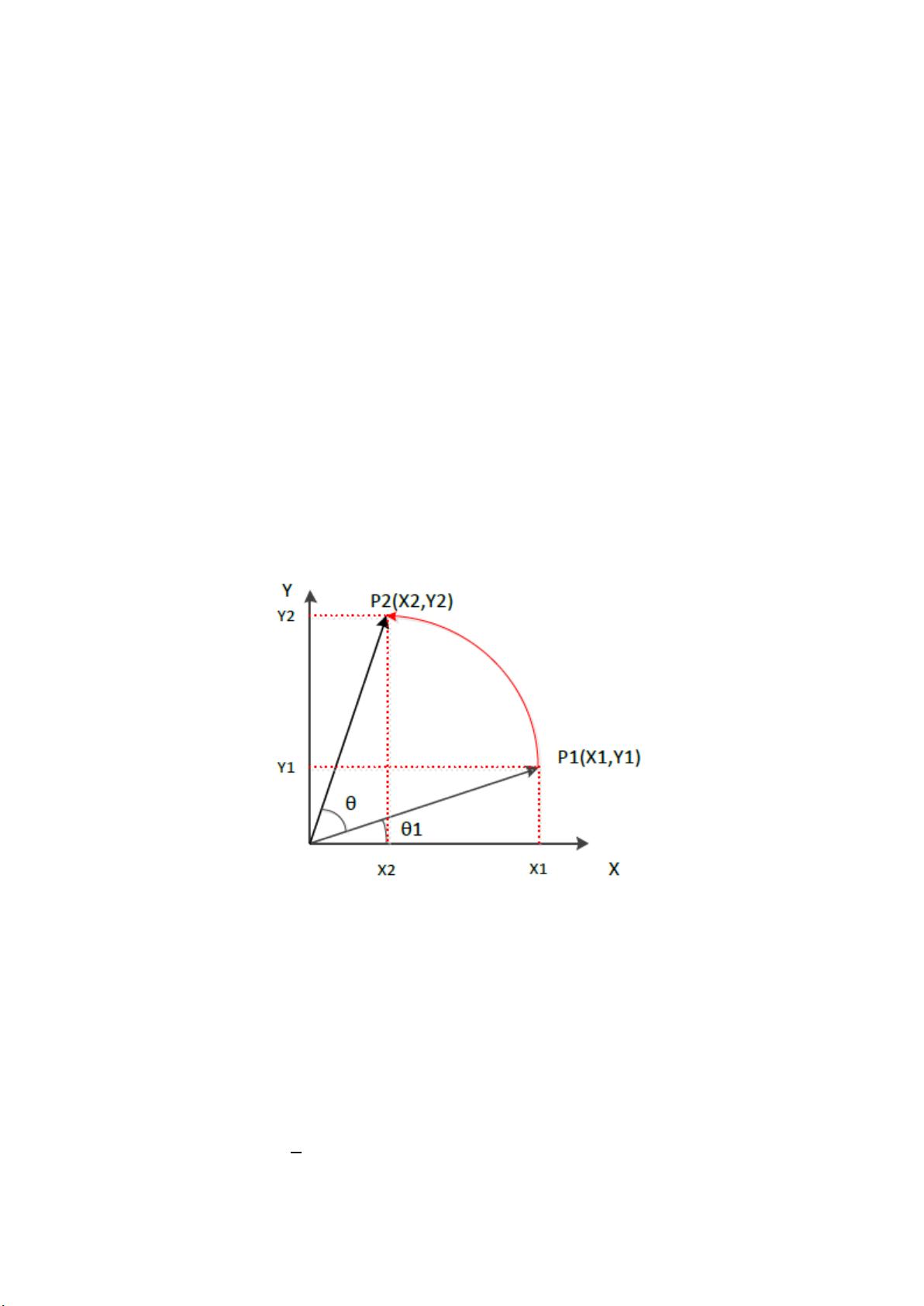
本文档主要探讨了迭代计算正余弦值的方法以及其在FPGA上的具体应用。首先，作者通过数学公式推导解释了如何通过迭代计算确定一个向量绕原点旋转特定角度后的坐标变化，这里的关键是利用三角函数的和角公式，将向量P1绕不同角度θi旋转后的坐标Xi和Yi表示为前一次旋转后的坐标加上修正项。作者特别提到，通过假设每个旋转角度θi满足特定的关系式TANθi=2-i，使得计算过程中可以利用位移操作（如算术右移）来简化计算，这对于在资源受限的FPGA环境中实现高效计算至关重要。 接着，作者列举了θi与TANθi的关系表，展示了随着i的增长，θi的值逐渐减小，TANθi则呈现出明显的下降趋势。这种假设使得在FPGA上处理连续的正余弦值计算时，可以通过预先计算出一组θi对应的TANθi值，然后根据实际的旋转次数进行查找和更新，从而减少了运算复杂度。 在FPGA的应用部分，文章着重讲述了如何将这个迭代计算过程应用于绝对式编码器解码后的余弦值计算。由于文中提到未使用预定义的IP核，这可能意味着作者设计了一个自定义的硬件模块，通过硬件级别的优化来实现快速、精确的正余弦值计算。这种方法对于需要高精度和实时性的伺服系统来说，具有很高的实用价值。 这份总结详细阐述了迭代计算在FPGA上的实际应用策略，包括数学模型构建、假设条件的选择、以及硬件实现的优化技巧，为读者提供了在有限资源下有效利用FPGA进行正余弦值计算的技术路径。对于从事FPGA开发或伺服系统设计的工程师而言，这篇文章提供了有价值的学习资料和实践经验。