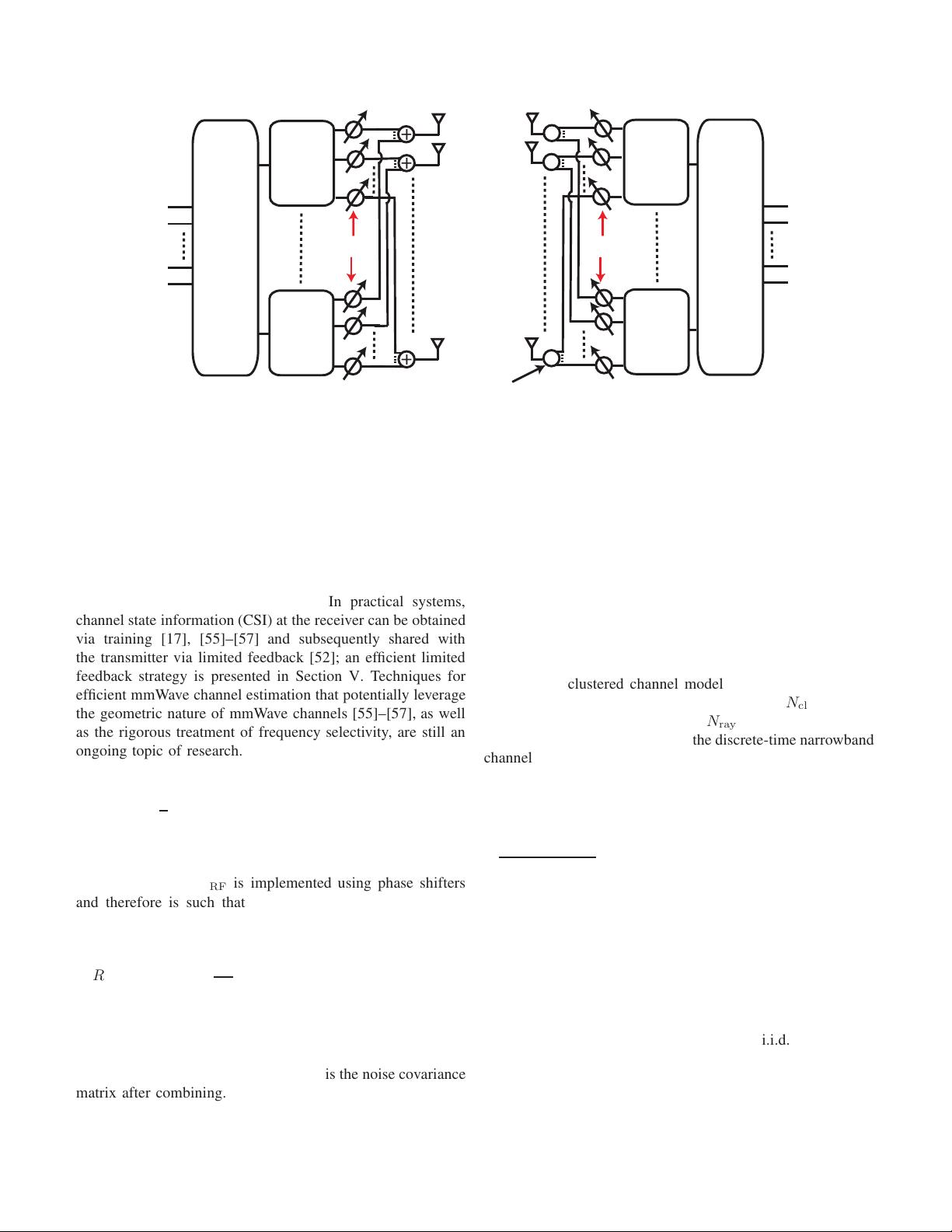
EL AYACH et al.: SPATIALLY SPARSE PRECODING IN MILLIMETER WAVE MIMO SYSTEMS 1501
RF
Chain
RF
Chain
Baseband
Precoder
F
BB
N
t
N
r
N
RF
t
N
s
RF
Chain
RF
Chain
Baseband
Combiner
W
BB
F
RF
W
RF
Digital
Analog DigitalAnalog
N
s
N
RF
r
splitters
Fig. 1. Simplified hardware block diagram of mmWave single user system with digital baseband precoding followed by constrained radio frequency precoding
implemented using RF phase shifters.
where y is the N
r
× 1 received vector, H is the N
r
× N
t
channel matrix such that E
H
2
F
= N
t
N
r
, ρ represents the
average received power, and n is th e vector of i.i.d CN(0,σ
2
n
)
noise. In writing (1), we implicitly assume perfect timing and
frequency recovery. Moreover, to enable precoding, we assume
that the channel H is known perfectly and instantaneously
to both the transmitter and receiver. In practical systems,
channel state information (CSI) at the receiver can be obtained
via training [17], [55]–[57] and subsequently shared with
the transmitter v ia limited feedback [52]; an efficient limited
feedback strategy is presented in Section V. Techniques for
efficient mmWave channel estimation that potentially leverage
the geometric nature of mmWave channels [55]–[57], as well
as the rigorous treatment of frequency selectivity, are still an
ongoing topic of research.
The receiver u ses its N
s
≤ N
RF
r
≤ N
r
RF chains and
analog phase shifters to obtain the processed received signal
y =
√
ρW
∗
BB
W
∗
RF
HF
RF
F
BB
s + W
∗
BB
W
∗
RF
n, (2)
where W
RF
is the N
r
×N
RF
r
RF combining matrix and W
BB
is the N
RF
r
× N
s
baseband combining matrix. Similarly to
the RF precoder, W
RF
is implemented using phase shifters
and therefore is such that (W
(i)
RF
W
(i)∗
RF
)
,
= N
r
−1
.When
Gaussian symbols are transmitted over the mmWave channel,
the spectral efficiency achieved is g iven by [58]
R =log
2
I
N
s
+
ρ
N
s
R
−1
n
W
∗
BB
W
∗
RF
HF
RF
F
BB
× F
∗
BB
F
∗
RF
H
∗
W
RF
W
BB
,
(3)
where R
n
= σ
2
n
W
∗
BB
W
∗
RF
W
RF
W
BB
is the noise covariance
matrix after combining.
B. Channel Model
The hig h free-space pathloss that is a characteristic of
mmWave propagation leads to limited spatial selectivity or
scattering. Similarly, the large tightly-packed antenna arrays
that are characteristic of mmWave transceivers lead to high
levels of antenna correlation. Th is combinatio n of tightly
packed arrays in sparse scattering environments makes many
of the statistical fading distributions used in traditional MIMO
analysis inaccurate for mmWave channel modeling. For this
reason, we adopt a narrowband clustered channel representa-
tion, based on the extended Saleh-Valenzuela model, which
allows us to accurately capture the mathematical structure
present in mmWave channels [28], [29], [31], [59], [60].
Using the clustered channel model, the m atrix channel H
is assumed to be a sum of the contributions of N
cl
scattering
clusters, each of which contribute N
ray
propagation paths to
the channel matrix H. Therefore, the discrete-time narrowband
channel H can be written as
H = γ
i,
α
i
Λ
r
(φ
r
i
,θ
r
i
)Λ
t
(φ
t
i
,θ
t
i
)a
r
(φ
r
i
,θ
r
i
)a
t
(φ
t
i
,θ
t
i
)
∗
,
(4)
where γ is a normalization factor such that γ =
N
t
N
r
/N
cl
N
ray
and α
i
is the complex gain of the
th
ray
in the i
th
scattering cluster, whereas φ
r
i
(θ
r
i
)andφ
t
i
(θ
t
i
)
are its azimuth (elevation) angles of arrival and departure
respectively. The functions Λ
t
(φ
t
i
,θ
t
i
) and Λ
r
(φ
r
i
,θ
r
i
) rep-
resent the transmit and receive antenna element gain at the
corresponding angles of departure and arrival. Finally, the
vectors a
r
(φ
r
,θ
r
) and a
t
(φ
t
i
,θ
t
i
) represent the normalized
receive and transmit array r esponse vectors at an azimuth
(elevation) angle of φ
r
i
(θ
r
i
)andφ
t
i
(θ
t
i
) respectively.
In Section VI, we assume that α
i
are i.i.d. CN(0,σ
2
α,i
)
where σ
2
α,i
represents the average power of the i
th
cluster. The
average cluster powers are such that
N
cl
i=1
σ
2
α,i
= γ where
γ is a normalization constant that satisfies E
H
2
F
=
N
t
N
r
[29]. The N
ray
azimuth and elevation angles of de-
parture, φ
t
i
and θ
t
i
, w ithin the cluster i are assumed to be
randomly distributed with a uniformly-random mean cluster
angle of φ
t
i
and θ
t
i
respectively, and a constant angular spread









