并行Skein哈希函数算法的效率优化
需积分: 9 173 浏览量
更新于2024-08-12
1
收藏 185KB PDF 举报
"这篇文档是关于一种针对 Skein 哈希函数的高效并行算法的研究，由 Kevin Atighehchi, Adriana Enache, Traian Muntean 和 Gabriel Risterucci 在 ERISCS 研究小组完成。文章讨论了如何在多核处理器上实现 Skein 的优化性能，以满足对关键应用的需求。"
Skein 是一种密码学哈希函数，最初作为 NIST 的 SHA-3 竞赛的候选算法之一。由于 MD4、MD5 和 SHA-0 等早期哈希函数的安全性受到挑战，NIST 发起了新的哈希函数标准制定过程，旨在设计出更安全且高效的算法。尽管 SHA-1 还未被完全攻破，但已经出现了一些减少其计算复杂度的碰撞寻找方法，这促使了 SHA-3 的诞生。
Skein 作为 SHA-3 竞赛的提案之一，以其独特的三鱼（Threefish）分组密码为基础，设计了一个灵活且可扩展的架构。它支持多种块大小和输出长度，可以提供不同级别的安全性。文章的核心是提出了一种并行算法，以利用现代多核心处理器的并行计算能力，提高 Skein 的执行效率。
并行化算法设计的目标是最大化多核处理器的性能，尤其是在处理关键任务时，这些任务通常需要高度优化的实施。文中介绍的初步工作是 Skein 的并行实现之一，也是该领域的早期尝试，对于理解如何有效地在多核环境中并行处理 Skein 算法具有重要意义。
作者们对并行算法进行了性能评估，这包括对算法的效率、吞吐量以及资源利用率的分析。通过这种方式，他们能够量化并行算法相对于单线程版本的改进，并为未来的设计提供指导。这样的研究对于提升加密算法在现代硬件上的性能至关重要，特别是在面对大数据和云计算等高计算需求场景时。
这篇文章探讨了如何通过并行计算来增强 Skein 哈希函数的性能，这对于理解和优化现代密码学算法在多核处理器上的表现有着重要的理论和实践价值。通过这样的工作，可以为未来的哈希函数设计和实现提供宝贵的经验和参考。
4 Hash Tree Mode
4.1 Specification
Tree processing varies according to the following input pa-
rameters:
Y
l
The leaf size encoding. The size of each leaf of the
tree is N
l
= N
b
2
Y
l
bytes with Y
l
≥ 1 (where N
b
is
the size of the internal state of Skein).
Y
f
The fan-out encoding. The fan-out of a tree node is
2
Y
f
with Y
f
≥ 1. The size of each node is N
n
=
N
b
2
Y
f
.
Y
m
The maximum tree height; Y
m
≥ 2. If the hieght of
the tree is not limited this parameter is set to 255.
G
0
The input chaining value and the output of the previ-
ous UBI function.
M The message data.
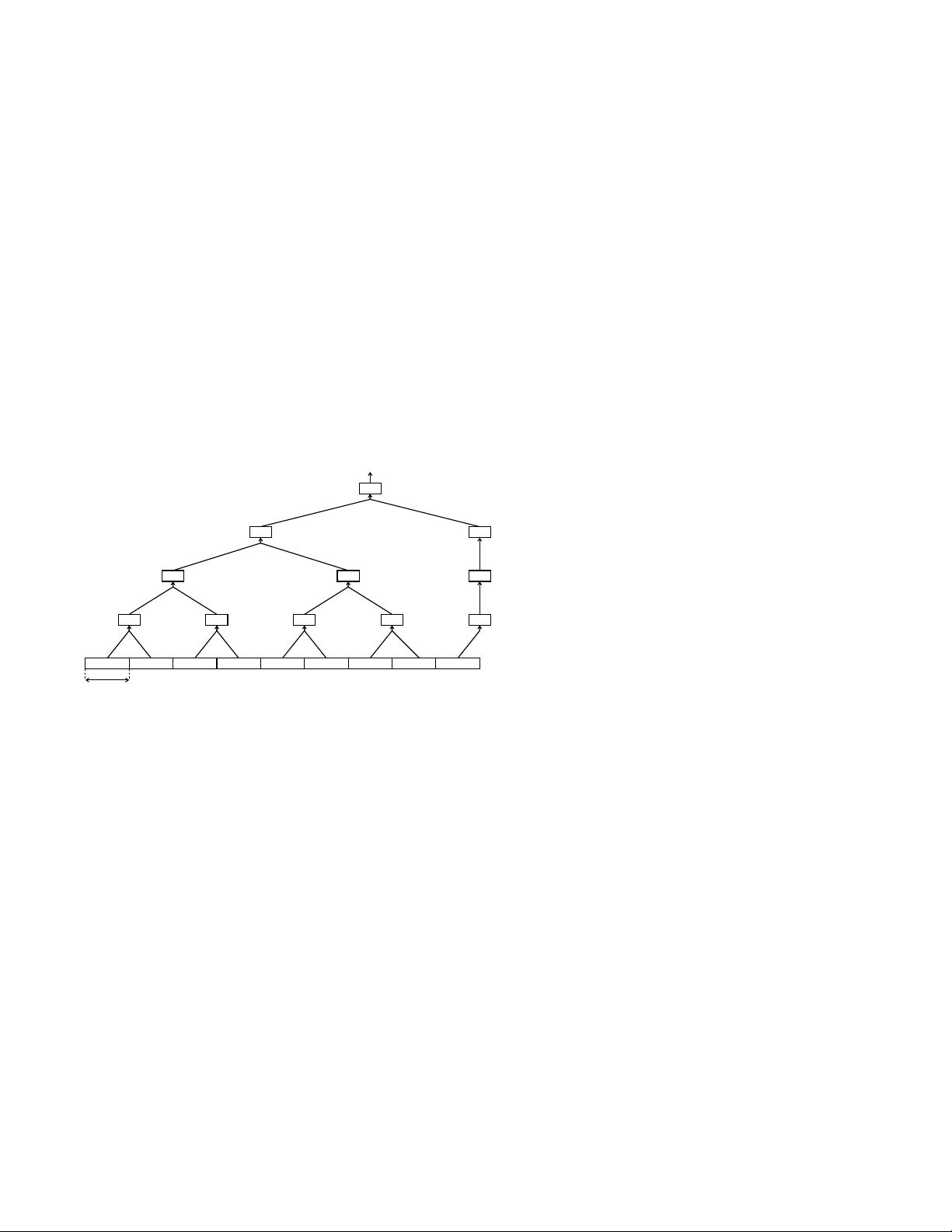
UBI UBI UBI UBI UBI
UBI
UBIUBI
UBI UBI
UBI
message
N
b
-sized
Figure 1: Tree hashing with Y
l
= Y
f
= 1
We define the leaf size N
l
= N
b
2
Y
l
and the node size
N
n
= N
b
2
Y
f
.
We first split the message M into one or more mes-
sage blocks M
0,0
, M
0,1
, ..., M
0,k−1
, each of size N
l
bytes
except the last, which may be smaller. We now define the
first level of tree hashing by:
M
1
=
k−1
n
i=0
UBI(G
0
, M
0,i
, iN
l
+ 1 · 2
112
+ T
msg
· 2
120
)
The rest of the tree is defined iteratively. For any level l =
1, 2, ... we use the following rules:
1. If M
l
has length N
b
, then the result G
0
is defined by
G
1
= M
l
.
2. If M
l
is longer than N
b
bytes and l = Y
m
−1, then we
have almost reached the maximum tree height. The
result is then defined by:
G
1
= UBI(G
0
, M
l
, Y
m
· 2
112
+ T
msg
· 2
120
)
3. If neither of these conditions holds, we create
the next tree level. We split M
l
into blocks
M
l,0
, M
l,1
, ..., M
l,k−1
, where all blocks are of size
N
n
, except the last which may be smaller. We then
define:
M
l+1
=
k−1
n
i=0
UBI(G
0
, M
l,i
, iN
n
+(l+1)·2
112
+T
msg
·2
120
)
and apply the above rules to M
l+1
again.
The result G
1
is then the chaining input to the output
transformation.
4.2 Sequential implementation
The straightforward method would consist of implement-
ing this algorithm as it is described in its specifications.
This implementation constitutes a scheduling method for
the node processing that we call Lower level and leftmost
node first (or Lower level node first for short). Such an
implementation has the disadvantage of consuming a lot
of memory. For instance if we take Y
l
= 1, we need an
amount of avalaible memory space of up to half of the
message size, which may be impossible for long messages.
There is an effective algorithm (see [13]) which computes
a value of a node of height h, while storing only up to h + 1
hash values. The idea is to compute a new parent hash
value as soon as possible before continuing to compute
the lower level node hash values; we call this method
heigher level node first. The interest of this method,
which maintains a stack in which the intermediate values
are stored, is to rapidly discard those that are no longer
needed. This stack, which is initially empty, is used as
follows: we use (push) leaf values one by one from left to
right and we check at each step whether or not the last two
values on the stack are of the same height. If such is the
case, these last two values are popped and the parent hash
value is computed and pushed onto the stack, otherwise we
continue to push a leaf value and so on. Note that we could
use a two hash-sized buffer at each level (from 1 to h)
instead of a unique stack, even though it is useless in such a
sequential implementation. This algorithm can be applyed
to Skein trees, in which case the memory consumption
does not exceed (h − 1)(2
Y
f
− 1) + 2
Y
l
blocks of size N
b
for the computation of a node of height h, on the condition
that we include a special termination round since they are
not necessarily full trees (as we can see in Figure 1).
We assume the existence of the following elements:
• oracles:
– S(n) which returns the node value.
– LEAF CALC(l) which returns a pair of ele-
ments (S(n
l
), t) where S(n
l
) is the leaf value
(a N
b
-sized block of the message) and t a binary
variable indicating whether it is the last leaf (1)
or not (0).
剩余10页未读，继续阅读
2017-11-03 上传
2017-09-27 上传
2018-03-19 上传
2023-09-06 上传
2023-05-23 上传
2023-05-12 上传
2023-06-06 上传
2023-06-10 上传
2023-10-18 上传
baidu_38409916
- 粉丝: 0
- 资源: 2
我的内容管理
展开
最新资源
- Java集合ArrayList实现字符串管理及效果展示
- 实现2D3D相机拾取射线的关键技术
- LiveLy-公寓管理门户：创新体验与技术实现
- 易语言打造的快捷禁止程序运行小工具
- Microgateway核心：实现配置和插件的主端口转发
- 掌握Java基本操作：增删查改入门代码详解
- Apache Tomcat 7.0.109 Windows版下载指南
- Qt实现文件系统浏览器界面设计与功能开发
- ReactJS新手实验：搭建与运行教程
- 探索生成艺术：几个月创意Processing实验
- Django框架下Cisco IOx平台实战开发案例源码解析
- 在Linux环境下配置Java版VTK开发环境
- 29街网上城市公司网站系统v1.0：企业建站全面解决方案
- WordPress CMB2插件的Suggest字段类型使用教程
- TCP协议实现的Java桌面聊天客户端应用
- ANR-WatchDog: 检测Android应用无响应并报告异常
