算法训练：求图中最大联合权值与总和

"这篇资源是关于算法训练的入门教程，主要涵盖了两个问题，分别是图论中的最短路径问题和模拟游戏策略的优化问题。" **第一题：最短路径与联合权值问题** 这是一个典型的图论问题，涉及到无向连通图的最短路径计算。给定一个无向图G，包含n个节点，节点编号从1到n，并且有n-1条边，每条边的权重为1。节点i的权值为Wi。问题的关键在于找到所有两点间距离为2的点对，它们之间的联合权值为Wu * Wv。 要解决这个问题，首先需要计算出任意两点间的最短路径。这可以通过Dijkstra算法或Floyd-Warshall算法实现。Dijkstra算法适用于单源最短路径问题，而Floyd-Warshall算法则能计算所有对之间的最短路径。在这道题目中，由于所有边的权重都为1，因此也可以使用BFS（广度优先搜索）来找到最短路径，因为对于边权重为1的图，BFS和Dijkstra算法的结果是一致的。 计算完所有点对的最短路径后，筛选出距离为2的点对，然后计算它们的联合权值。最后找出联合权值的最大值和所有联合权值的和，并对10007取余。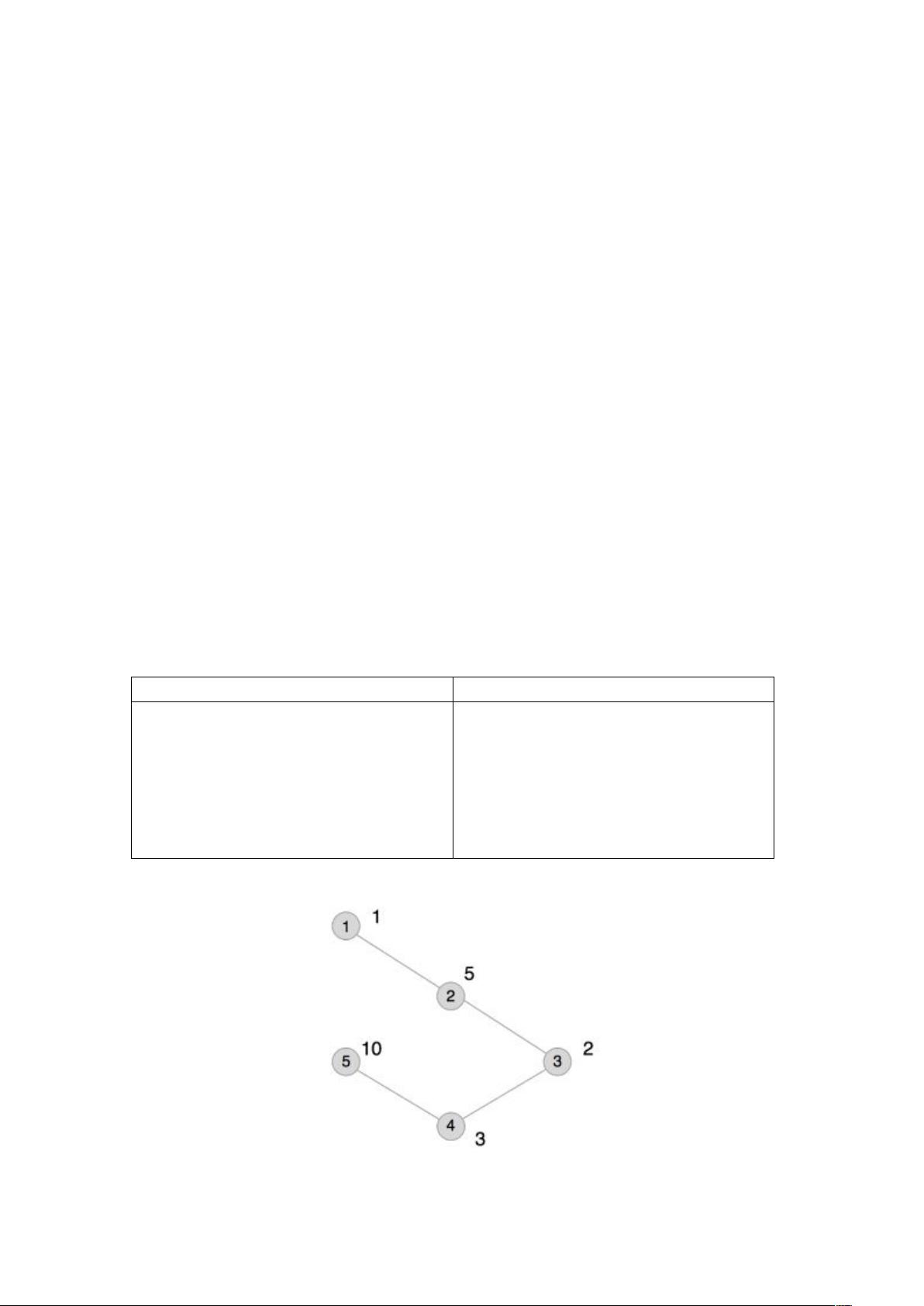 **样例分析** 给定的例子中，图G有5个节点，通过构建邻接矩阵或邻接表表示图。通过BFS或Dijkstra算法，我们可以找到每个节点到其他节点的最短距离。在样例中，存在多个距离为2的点对，例如(1, 3)和(2, 4)等。计算它们的联合权值，找出最大值并求和，最后输出这两个结果。 **第二题：Flappy Bird 游戏策略模拟** 这个问题是一个简化版的Flappy Bird游戏模拟，玩家需要控制小鸟通过固定位置的管道。游戏简化为二维平面，小鸟在横坐标方向上以恒定速度移动，而在纵坐标方向上可以通过点击屏幕改变飞行高度。 要解决这个问题，可以采用动态规划或贪心策略。动态规划方法可以考虑所有可能的点击序列，计算每个状态（小鸟的位置和高度）的最佳操作。贪心策略则可能考虑在特定高度点击以达到最大可能的通过管道的概率。 在实际应用中，可能需要结合物理模型，考虑到小鸟上升和下降的速度以及重力的影响。可以建立数学模型，对每一步的操作进行模拟，以找到通过所有管道的最优策略。 这两个问题都需要运用计算机科学的基本算法和逻辑思维能力，是提升算法能力和编程技能的良好练习。