Kahn算法与字典序最小拓扑排序：DAG的高效求解

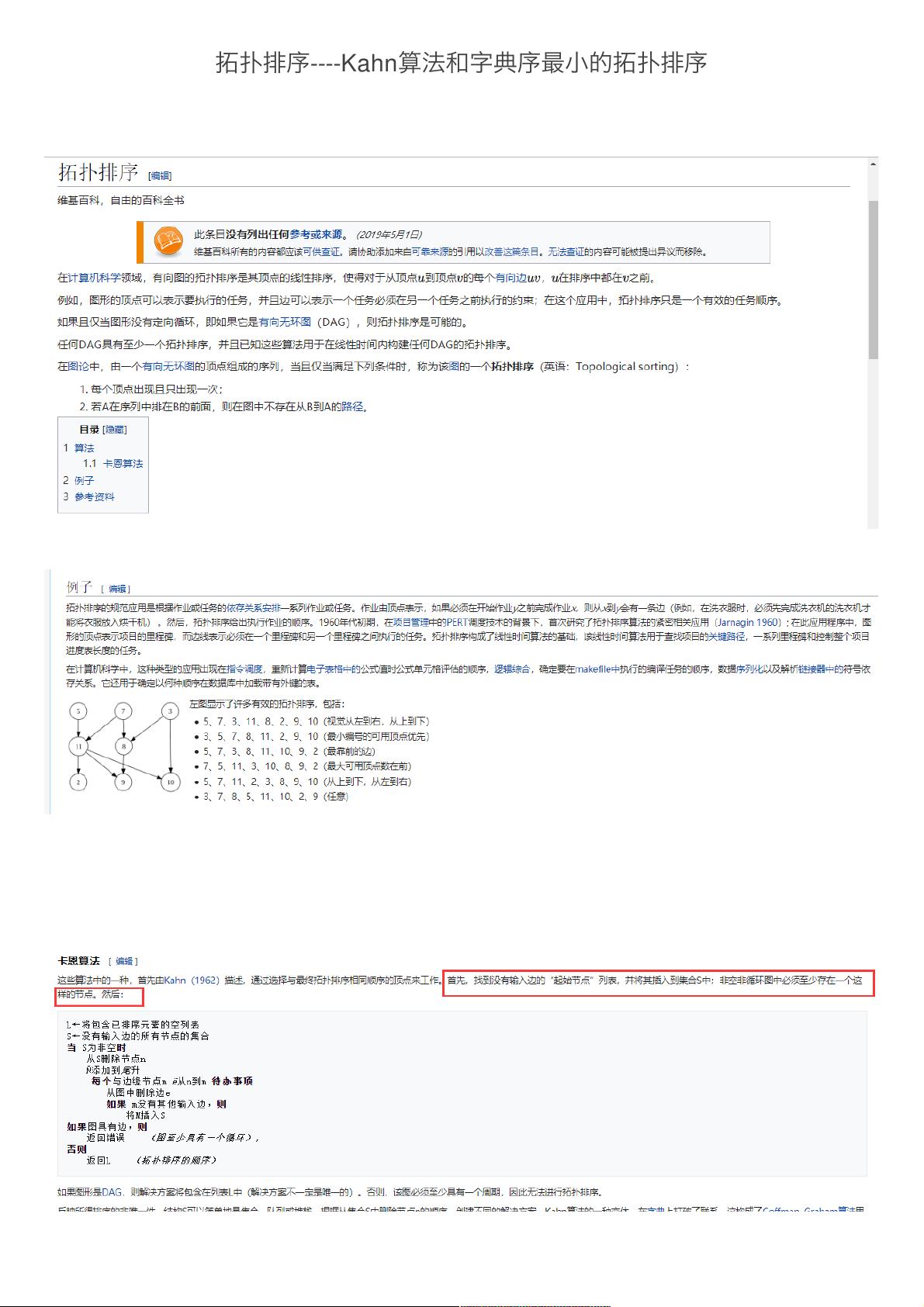
拓扑排序是一种在有向无环图(DAG)中确定节点顺序的方法，使得对于图中的任意节点u，其在排序后的列表中都出现在所有指向它的节点之后。本文主要讨论的是Kahn算法，这是一种高效的拓扑排序算法，以及如何实现字典序最小的拓扑排序。 **一、拓扑排序定义** 拓扑排序的目标是为图中的节点分配一个顺序，使得对于每条有向边(u, v)，节点u总是在节点v之前。在无环图中，这样的排序总是存在的。若图中存在环，则无法进行拓扑排序，因为环会导致无法确定节点的相对位置。 **二、Kahn算法介绍** Kahn算法的关键在于逐步选择入度为0的节点，并调整它们的相邻节点的入度，直到所有节点都被处理。算法步骤如下： 1. 初始化：统计每个节点的入度（即入边数量），并标记所有入度为0的节点。 2. 从入度为0的节点开始，将它们加入队列，并递增访问计数。 3. 取出队首节点，添加到排序结果列表（L）的末尾，然后检查与该节点相连的节点，移除边并减少连接节点的入度。 4. 如果某个节点的入度变为0，将其加入队列。 5. 重复步骤3和4，直到队列为空。若访问节点数小于图节点总数，意味着图中存在环，无法进行拓扑排序。 6. 如果算法成功执行，返回排序后的列表L。 **三、Kahn算法伪代码** Kahn算法的伪代码展示了整个过程，包括创建空列表L，维护一个无入度节点集合S，以及遍历节点直至完成排序或检测环。 **四、代码实现** 给出的代码片段展示了使用C++实现Kahn算法的部分结构，包括定义图类（Graph），其中包含顶点数n、邻接表表示法以及Graph构造函数。在这个类中，会处理节点的入度计算、入队、出队以及边的操作，以实现Kahn算法的核心逻辑。 字典序最小的拓扑排序是指在所有可能的拓扑排序中，找到一个序列，使得对于任意两个节点i和j，如果节点i在节点j的前面，那么所有从i到j的路径上节点的编号也是从小到大排列的。这通常通过调整Kahn算法中的插入顺序来实现，确保在遍历过程中尽可能早地添加较小的节点。 总结来说，Kahn算法是解决拓扑排序问题的有效工具，它利用图的特性，按照特定规则逐步构建拓扑排序。通过理解其原理和伪代码，开发者可以实现这个算法并应用到实际的编程项目中，特别是在处理依赖关系、任务调度等场景时。同时，对于字典序最小的拓扑排序，算法的优化可以提升排序结果的可读性和一致性。