哈工大机器学习课件：概率与不确定性解析

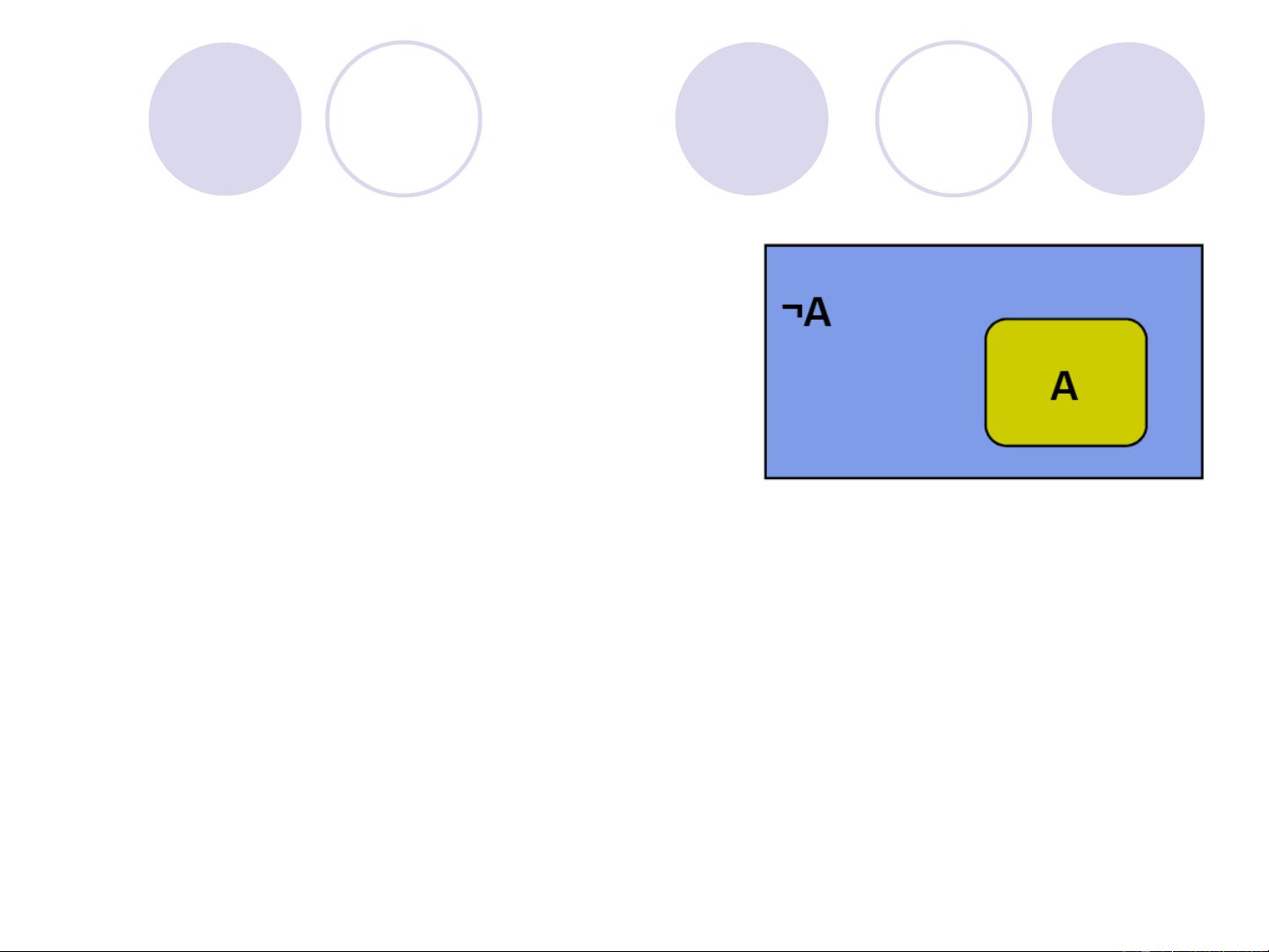
"哈工大机器学习课件-2，主要涵盖了概率论在机器学习中的应用，基于Bishop的《Pattern Recognition and Machine Learning》一书的第1、2章内容。" 本文将深入探讨机器学习中概率论的基础概念及其重要性。在机器学习领域，特别是在处理不确定性时，概率论扮演着至关重要的角色。不确定性可能源于传感器测量的噪声、观察的不完全性或训练数据的有限样本大小。概率论提供了一种量化不确定性的方法。 首先，概率的基本概念包括可重复实验，它具有随机的试验结果。每次试验的结果集称为样本空间(S)，可以是有限的也可以是无限的。事件A是样本空间S的任意子集，代表着可能发生的特定情况。 接着，我们介绍了两种概率定义。第一种是古典定义：一个事件A的概率是其发生次数与总试验次数的极限比值，即相对频率。这在长期重复的试验中趋向稳定。第二种是公理化（Kolmogorov）定义，它更抽象且系统化。根据这个定义，事件A的概率P(A)是一个满足0≤P(A)≤1的实数，确保了概率值在0到1之间。同时，空集的概率P(ϕ)被定义为0，表示没有结果发生的概率为0。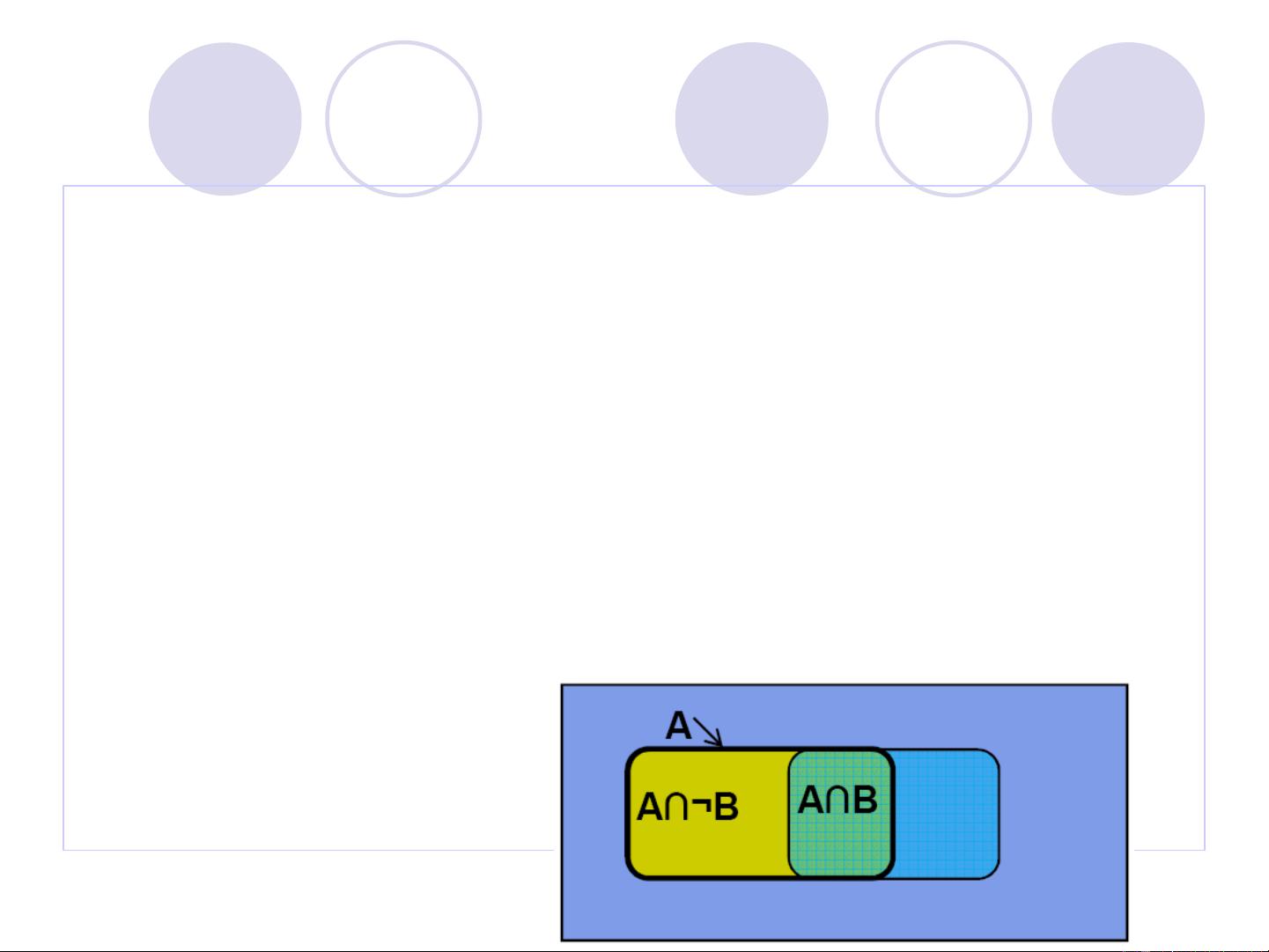 在机器学习中，概率论的一些关键概念如条件概率、联合概率、边缘概率以及贝叶斯定理是理解许多算法的基础，例如朴素贝叶斯分类器、最大似然估计以及马尔科夫决策过程等。条件概率P(A|B)表示在已知事件B发生的情况下，事件A发生的概率。联合概率P(A,B)描述的是事件A和事件B同时发生的概率，而边缘概率P(A)则是事件A发生的概率，不考虑其他事件。 此外，概率分布，如伯努利分布、二项分布、泊松分布和高斯（正态）分布等，是机器学习中建模和分析数据的基础。例如，二项分布常用于描述独立重复试验的成功次数，而高斯分布则广泛应用于描述自然现象的连续变量，如均值和方差。 概率论还为机器学习提供了理论框架，如最大后验估计（MAP）和贝叶斯推理。这些方法在参数估计、模型选择和不确定性量化等方面具有广泛的应用。 哈工大的这个机器学习课件部分强调了概率论在理解和解决机器学习问题中的核心地位，通过深入学习这部分内容，可以更好地理解和应用各种机器学习算法，以处理实际问题中的不确定性。