傅里叶变换与FFT算法在MATLAB和C语言中的应用

"傅里叶变换的应用及MATLAB、C语言程序实现" 傅里叶变换是一种重要的数学工具，广泛应用于信号处理、图像分析、通信工程等领域。它能将一个时域上的信号转换到频域，揭示信号的频率成分。在本文中，我们将探讨如何利用快速傅里叶变换（FFT）来计算连续时间信号的傅里叶变换，并在MATLAB和C语言环境中实现这一过程。 首先，傅里叶变换定义为： \[ X(\omega) = \int_{-\infty}^{\infty} x(t) e^{-j\omega t} dt \] 在实际应用中，我们通常采用离散形式，因为大多数信号都是通过采样获得的。当信号在每个时间间隔 \( T \) 内变化不大时，可以使用以下近似： \[ X(\omega) \approx \sum_{n=0}^{N-1} x(nT) e^{-j\omega nT} \] 其中，\( N \) 是采样点的数量，\( \Gamma \) 是一个固定的正实数，\( \omega \) 是频率变量，\( x(nT) \) 是采样信号。 当 \( \omega = \frac{2\pi k}{N T} \) 时，我们可以将上式转换为离散傅里叶变换（DFT）的形式： \[ X[k] = \frac{1}{N} \sum_{n=0}^{N-1} x[n] e^{-j\frac{2\pi kn}{N}} \] 其中，\( X[k] \) 表示离散傅里叶变换的结果，\( k \) 是频率索引。 使用FFT算法，可以高效地计算DFT。FFT是一种基于分治策略的算法，它将DFT的计算复杂度从线性降低到对数级别。在MATLAB中，可以使用`fft`函数来计算DFT，而在C语言中，可以使用库函数如`fftw`来实现相同的功能。 对于连续时间信号 \( x(t) \)，如果其带宽小于 \( B \)，则奈奎斯特定理建议采样频率至少为 \( 2B \)。这意味着采样间隔 \( T \) 应该小于 \( \frac{1}{2B} \)。如果信号仅在某个有限的时间区间 \( [0, t_s] \) 内存在，可以通过在 \( t > t_s \) 的位置补零来确保足够的采样点数 \( N \)。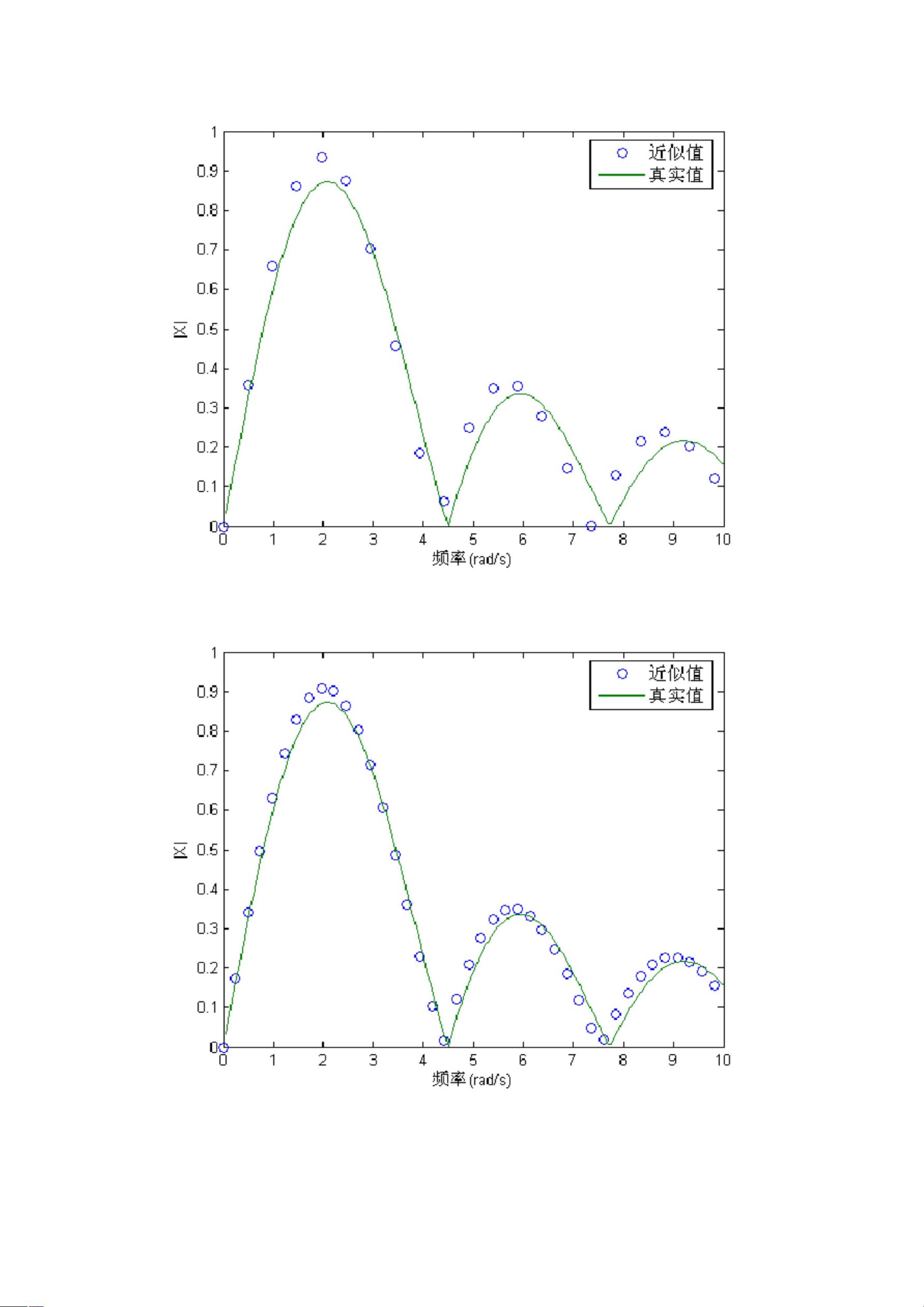 在MATLAB中，可以使用以下代码来计算傅里叶变换： ```matlab N = 1024; % 采样点数 T = 1/200; % 采样间隔 t = 0:T:(N-1)*T; % 时间轴 x = ...; % 定义信号x(t) X = fft(x); % 计算傅里叶变换 ``` 在C语言中，使用`fftw`库，代码可能如下： ```c #include <fftw3.h> #define N 1024 double x[N]; // 信号数组 fftw_complex X[N]; // 复数数组用于存储结果 fftw_plan p; // 初始化和计算 p = fftw_plan_dft_r2c_1d(N, x, X, FFTW_ESTIMATE); fftw_execute(p); // X[k] 现在包含了傅里叶变换的结果 ``` 以上讨论了如何使用FFT计算连续时间信号的傅里叶变换，并在MATLAB和C语言环境下实现。需要注意的是，实际计算得到的傅里叶变换 \( X(\omega) \) 或 \( X[k] \) 只是近似值，通过增加采样点数或减小采样间隔可以获得更精确的结果。在具体应用时，应根据信号特性选择合适的采样参数。