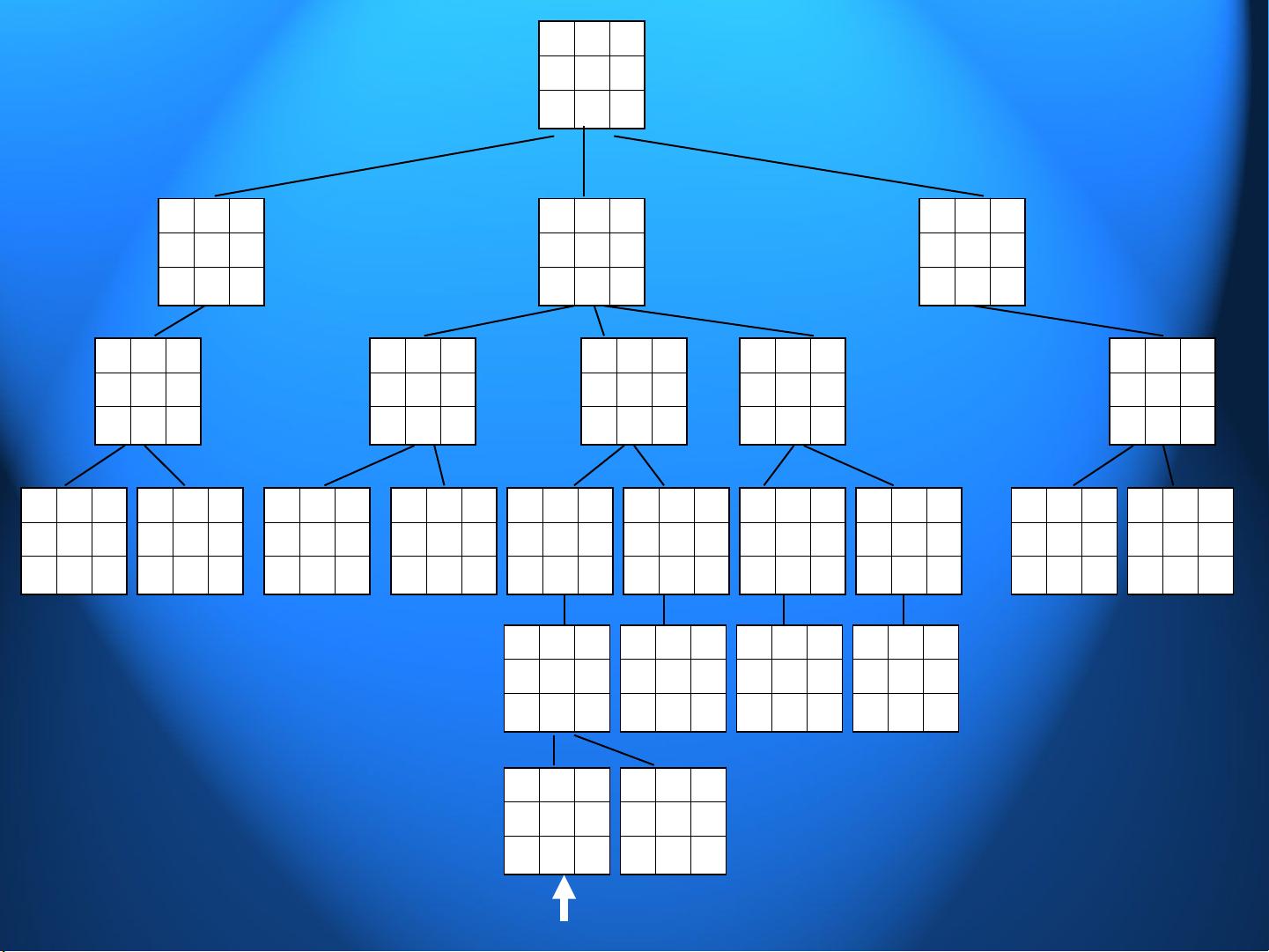
广度优先搜索:8数码问题的最小步数解法
广度优先搜索(BFS)是一种用于解决图或树搜索问题的经典算法,尤其在求解八数码问题(也称作15 puzzle)时非常适用。八数码问题是基于一个3x3的棋盘,其中8个数字按照1-8编号,有一个空位。目标是通过最少的步数将棋子移动到正确的位置,使得棋盘恢复成目标布局。
在BFS中,搜索过程从起始状态(初始布局)开始,逐层展开搜索树,即首先探索当前层的所有可能状态,然后才进入下一层。搜索树中的每个状态被视为一个节点,相邻的状态通过移动一个棋子的步骤连接,形成树状结构。BFS的优势在于确保了找到的是最短路径,因为它是按照步数的增加顺序来遍历节点的。
在处理八数码问题时,BFS的具体步骤如下:
1. **定义状态空间**:构建所有可能的棋盘状态集合,包括初始状态和目标状态,以及通过一次、两次移动等可能的中间状态。
2. **搜索算法**:从初始状态开始,依次对每一层的节点进行深度优先遍历。对于每个节点,尝试将空位与周围可移动的棋子交换位置,并生成新的状态。如果新状态等于目标状态,则找到了解决方案,记录下移动步数并停止搜索;否则,继续对新状态进行相同的操作。
3. **剪枝策略**:虽然BFS不涉及剪枝,但可以通过记忆化搜索(如A*搜索)来优化性能,避免重复计算已探索过的状态。
4. **结果输出**:当找到目标状态时,返回所经历的最小步数,这是最优解,因为BFS保证了找到的第一个目标是最优解。
5. **效率分析**:BFS的时间复杂度为O(b^d),其中b是每层的节点数量,d是搜索树的最大深度。由于八数码问题的棋盘大小固定,搜索深度通常是较小的,所以BFS在该问题上的表现通常较为高效。
举例中的过渡状态展示了从初始状态到目标状态可能经过的一系列变化,展示了BFS的搜索过程是如何逐步接近目标的。这种方法在计算机科学和人工智能领域广泛应用,特别是在求解类似迷宫导航、游戏AI等领域的问题时,广度优先搜索能够提供有效且直观的解决方案。
2010-09-29 上传
2023-09-19 上传
2008-12-29 上传
2022-09-24 上传
2009-01-02 上传
2009-10-22 上传
hongqiangcao
- 粉丝: 0
- 资源: 6
最新资源
- pyg_lib-0.3.1+pt20cpu-cp38-cp38-linux_x86_64whl.zip
- UnwelcomeCaller:在 Android 手机上分享有关不受欢迎来电者的信息
- vendor-directory-api:api访问供应商目录V1.0功能
- cd_app:仍在巩固节点技能
- action-release-download:GitHub Action下载发行工件
- WPFBasics-1:https://www.youtube.comwatch?v = Vjldip84CXQ&list = PLrW43fNmjaQVYF4zgsD0oL9Iv6u23PI6M&index = 1&ab_channel = AngelSix
- UNA-Bravo:国立大学课堂中的 Grupo Bravo 远程存储库
- ANNOgesic-0.7.27-py3-none-any.whl.zip
- zeal-redux-utils:使用Redux的实用程序功能
- netlifyTest
- Tieba_Sign-Go---Copy:百度贴吧 云签到
- 计时器
- COMP9220_Gomoku
- sass-jest:Jest中的Sass单元测试
- libCplus:精彩的库,用C语言提供了许多有用的功能,算法和数据结构,将其与-l9wada链接
- folk-website