Dijkstra算法C语言实现

"这篇资源提供了一个C语言实现的Dijkstra算法源代码，适用于寻找图中最短路径问题。" Dijkstra算法是一种经典的图论算法，由荷兰计算机科学家艾兹格·迪科斯彻在1956年提出，主要用于解决单源最短路径问题。这个算法的主要目标是从一个特定的起点（源节点）开始，逐步找到到达图中所有其他节点的最短路径。在实际应用中，Dijkstra算法常用于路由选择、网络流量优化和路径规划等领域。 在给出的源代码中，可以看到以下主要结构： 1. `struct Point`：表示图中的节点，包含节点名称（`vertex`）和指向相邻节点的链接列表（`work`）。 2. `struct Link`：表示节点之间的边，包含相邻节点名称（`vertex`）和边的权重（`value`）。 3. `struct Table`：工作表，用于记录当前已知最短距离的节点信息，包括距离（`cost`）、是否已知（`Known`）、节点名称（`vertex`）、路径（`path`）和指向下一个节点的指针（`next`）。 4. 函数`Dijkstra`：Dijkstra算法的核心实现，它接受图的节点列表和工作表作为参数，返回最短路径信息。 5. 函数`FindSmallest`：查找工作表中具有最小距离的节点。 6. 函数`CreateTable`：创建工作表，初始化每个节点的距离为无穷大（表示未访问）。 7. 函数`PrintTable`和`PrintPath`：分别用于打印工作表和最短路径信息。 源代码的运行过程如下： - 初始化所有节点距离为无穷大，将起点距离设为0，并将其添加到工作表。 - 在每次迭代中，`FindSmallest`函数找出工作表中距离最小的节点，然后更新与该节点相邻且未访问过的节点的距离。 - 当工作表为空或已访问完所有节点时，算法结束。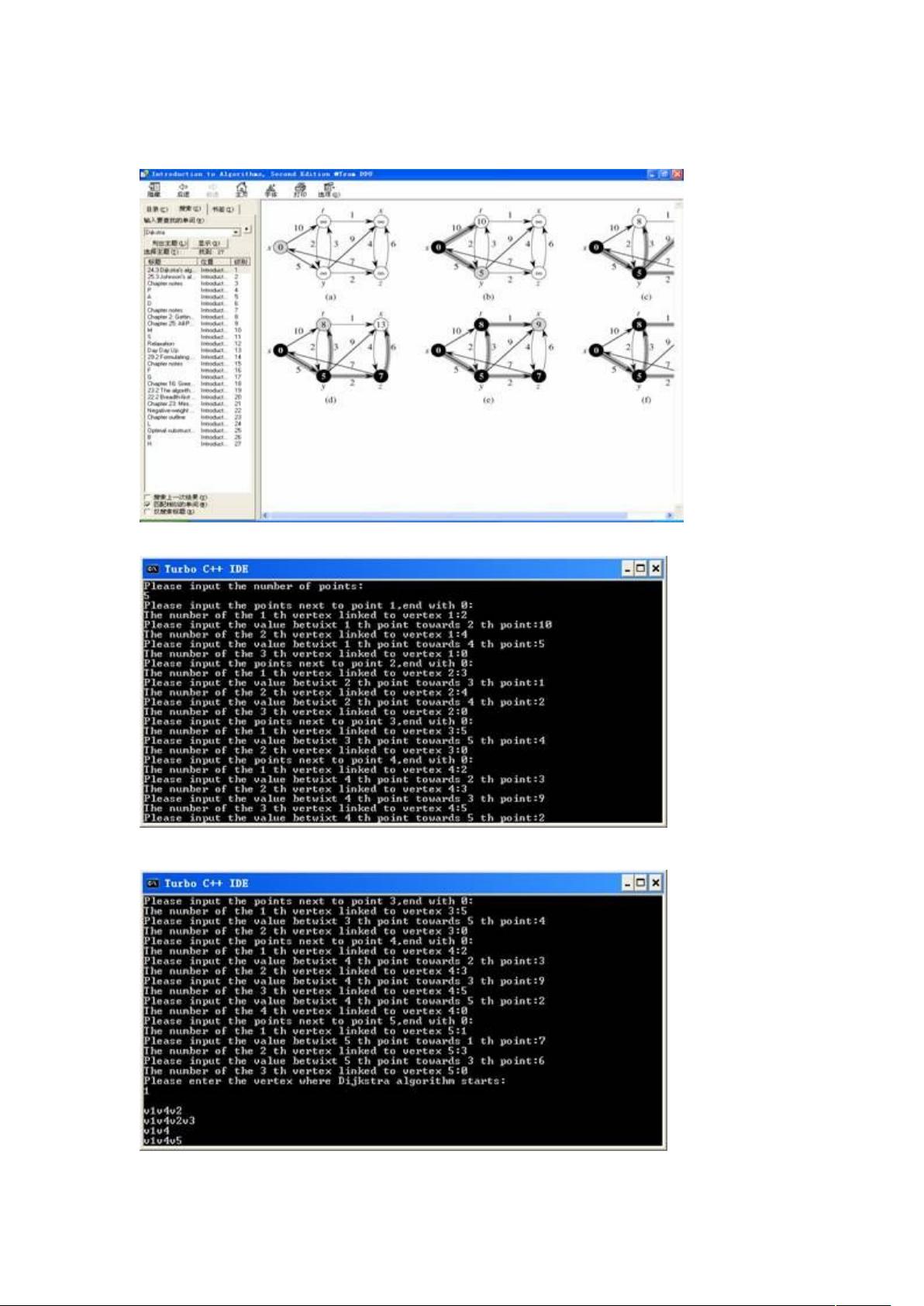 输入格式遵循特定规则，例如使用数字1到5分别代表s、t、x、y、z五个点，根据提示输入算法的起始点。输出则显示了从起点到各个节点的最短路径。 在实际应用中，Dijkstra算法的一个关键限制是它不能处理负权边，因为算法假设边的权重总是非负的。如果图中存在负权边，可能会导致算法无法找到正确的最短路径。对于这类情况，可以考虑使用其他算法，如Bellman-Ford算法。 这个C语言实现的Dijkstra算法提供了一个清晰的框架来解决单源最短路径问题，对于学习和理解Dijkstra算法的运作原理非常有帮助。