二维时空全息熵锥的动态性研究

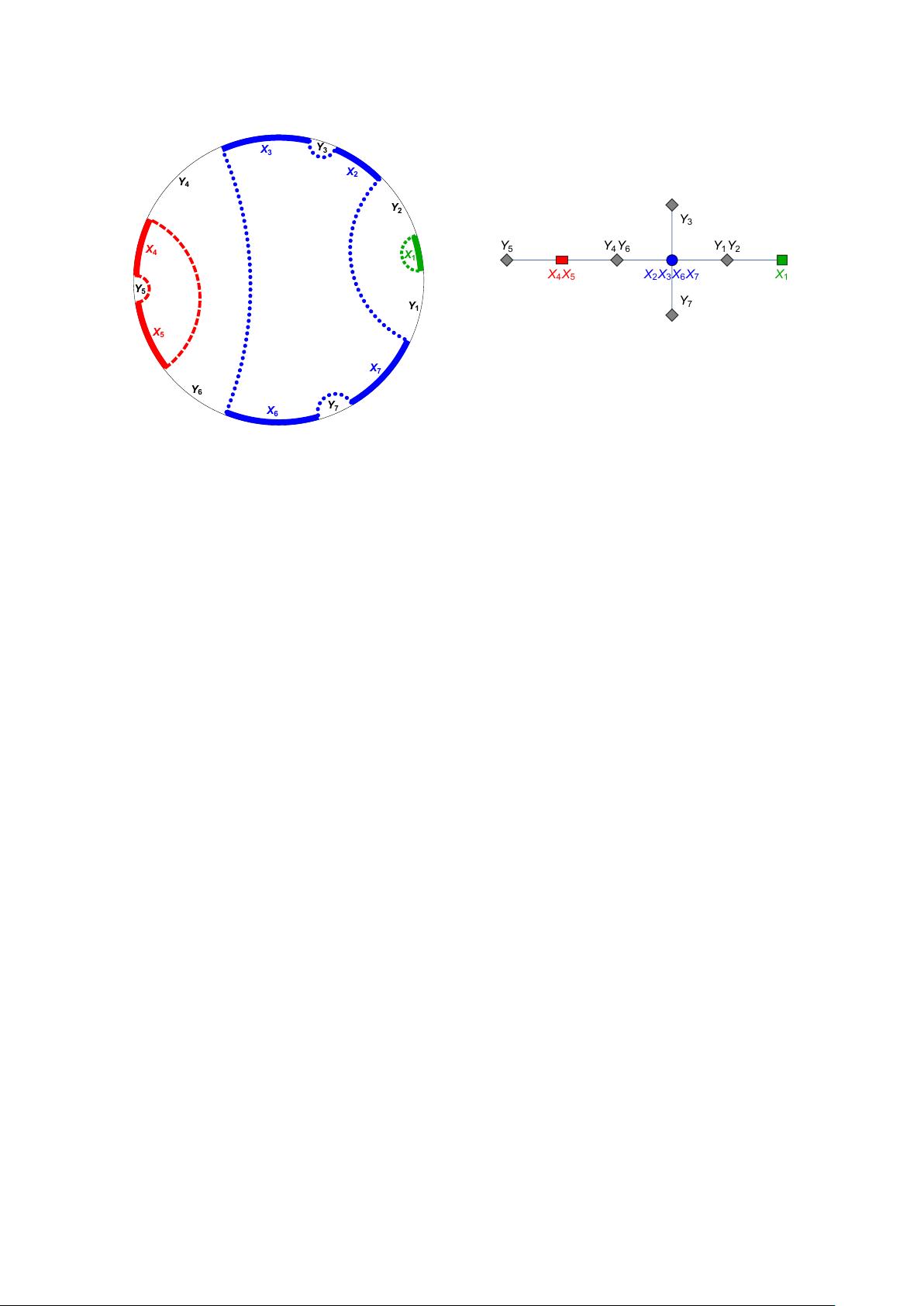
"这篇研究论文探讨了全息熵锥在二维时空中的时间依赖性，它深化了我们对全息对偶的理解，特别是关于边界状态的纠缠熵如何在动态环境中受到限制。作者Bartlomiej Czech和Xi Dong指出，全息熵锥是一组不等式，这些不等式在全息对偶理论中描述了边界状态的纠缠熵行为。Ryu-Takayanagi提议提供了一个几何框架，将边界理论的纠缠熵与bulk几何关联起来。" 在全息对偶理论中，一个关键的概念是Ryu-Takayanagi(RT)公式，它提出了一个关系，即一个量子场论的纯态在某个区域的纠缠熵可以被其AdS(反德西特)空间中的相应最小面积表面所计算。这一公式为理解复杂系统的纠缠提供了强有力的工具，尤其是在高维量子系统和引力理论之间的对应关系中。 论文中提到的“全息熵锥”是这些不等式的集合，它们规定了在给定理论中可能的纠缠熵值。在静态几何假设下，通过收缩图方法已经证明了一系列这样的不等式。收缩图方法是一种利用图论来计算量子系统纠缠熵的技术，特别适用于静态背景下的全息场景。 然而，现实世界中的物理过程往往不是静态的，因此研究动态全息状态的纠缠熵显得尤为重要。作者们通过引入“动力学空间技术”，成功地扩展了静态情况下的熵不等式证明，将它们应用到具有时间依赖性的全息状态。这一突破性的进展意味着在二维边界（对应三维bulk）的全息对偶中，我们能够理解和约束动态环境下的熵行为。 关键词包括“AdS-CFT对应”和“规范-引力对应”，表明这项工作与著名的AdS/CFT对应有关，这是弦理论和量子场论之间的一种精确对应，其中AdS空间的引力理论可以被一个边界上的无引力量子场论所描述。通过这种对应，二维边界上的时间依赖性纠缠熵问题可以映射到三维bulk的引力问题，从而在更广阔的背景下理解这些不等式的适用性。 这篇论文为全息对偶理论提供了新的洞察，不仅加深了我们对静态全息熵锥的理解，而且将其扩展到了更真实世界的动态场景，这在量子信息处理、黑洞物理和量子引力研究等领域具有重要意义。